Wolfram Demonstrations Project

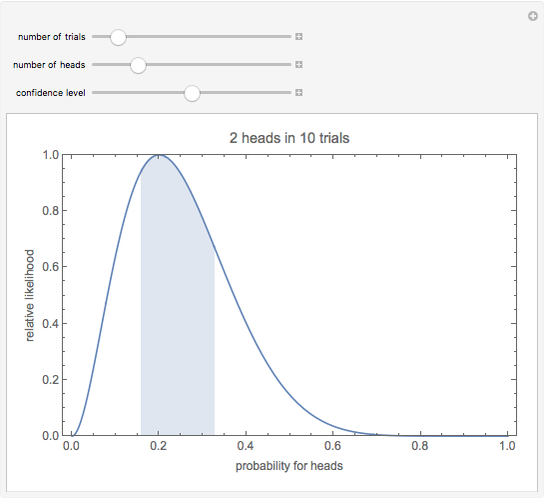
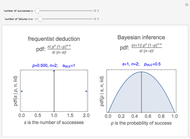
This Demonstration estimates the probability

that a biased coin will come up heads from a series of flips, using the maximum likelihood method. This method estimates

from the peak of the plotted curve, which shows the relative likelihood of

based on the number of heads observed in the series of flips. The shaded area represents a 95% confidence interval for the probability. 95% of all confidence intervals constructed in this manner would contain the true value of

Contributed by: Tad Hogg

Gamepad Controls

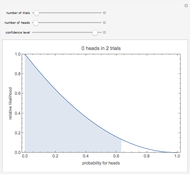
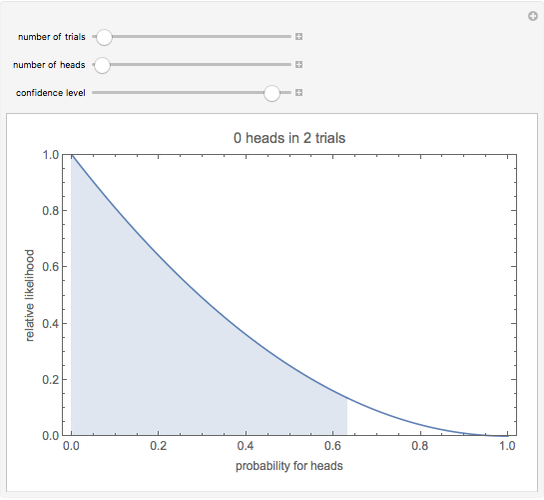
Snapshot 1: Observing no heads in two trials has maximum likelihood estimate

, but with a wide confidence interval: for 95% confidence we can only say the probability is less than 0.63.

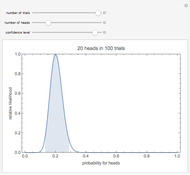
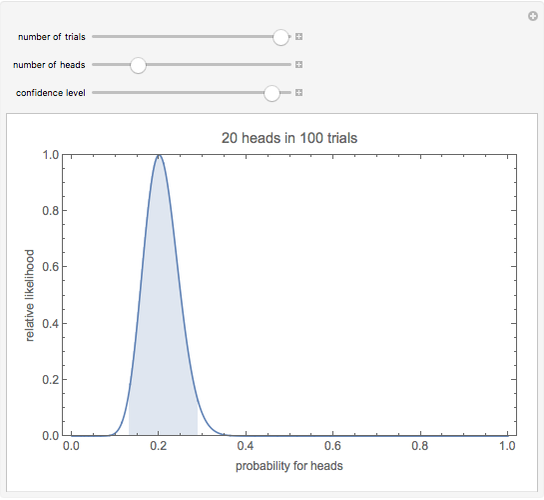
Snapshot 2: Observing 20 heads in 100 trials has maximum likelihood estimate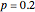

, the same as observing two heads in 10 trials. But the 95% confidence interval is much smaller: between 0.13 and 0.29.

Snapshot 3: Observing two heads in 10 trials shows a narrow confidence interval that corresponds to a low confidence level: the 50% confidence interval is between 0.16 and 0.33.

Flipping a biased coin

times gives

heads with probability

, the binomial distribution, where

is the probability that a flip gives heads. An unbiased coin has

Estimating the probability

is the inverse problem: we observe

heads in

trials and want to determine the unknown probability

and the accuracy of the estimate. The maximum likelihood estimate is the value of

giving the largest probability for the observed data. Treating the binomial distribution as a function of

, this procedure maximizes the likelihood, proportional to

. Viewed as a distribution on the unknown parameter

with given values of

and

, the likelihood is proportional to the beta distribution, with parameters

and

. The maximum of the likelihood occurs at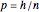

. For the plots, the likelihood is normalized so that its largest value is 1.

The confidence interval characterizes the accuracy of the maximum likelihood estimate. For a confidence level

between 0 and 1, the confidence interval gives a range of probabilities that contains the actual value with probability

. The interval covers a fraction

of the area under the likelihood curve shown in the plot.

The precise choice of confidence interval is somewhat arbitrary. Here the interval excludes equal area tails on each side of the distribution (except when

, in which case the maximum likelihood estimate is 0 or 1, respectively, and the shaded area is a one-sided interval). With this choice for the interval, if the actual probability value