Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Quarter-Car Suspension Model with Double Spring

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

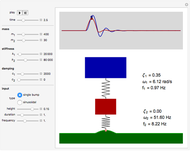
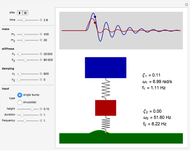
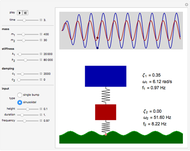
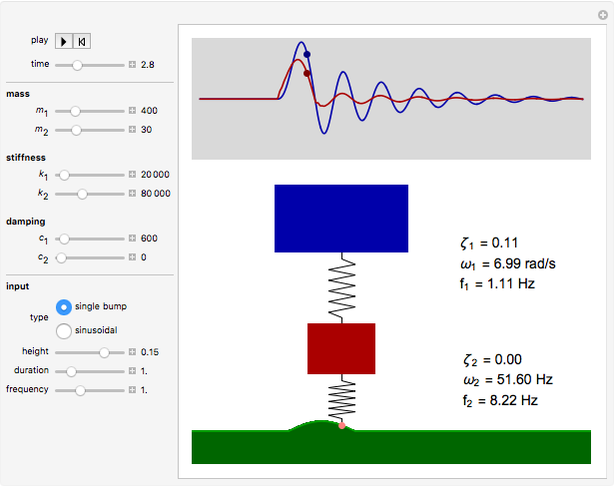
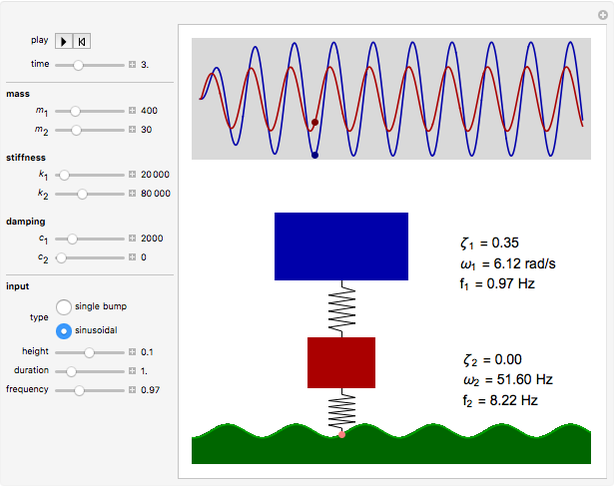
The quarter-car suspension model simulates a double-spring mass system. The mass attached to the spring represents the body of the car while the free mass represents the wheel, tire, and suspension.

[more]

The effect of an input from a single road hump or from a continuous sinusoidal input are simulated with graphical and animated representation of the system response. You can control the masses, stiffness, and damping for each spring and the input data.

[less]

Contributed by: Jon Neades (January 2014)
Open content licensed under CC BY-NC-SA

Snapshots

Details

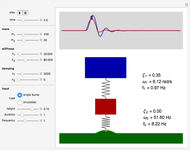
Snapshot 1: single road hump response from a system using typical parameters

Snapshot 2: response of an underdamped system to a single road hump

Snapshot 3: response to continuous input at resonant frequency of mass attached to spring

Snapshot 4: interference effects with no damping

The Demonstration solves the two second-order differential equations that describe a double-spring system:

,

.

The forcing function is modeled as either a single cosine shaped bump, such as a road speed hump, or a continuous sinusoidal input. A numerical solution is employed to show the evolution of the system.

This Demonstration was inspired by "Simulating Vehicle Suspension with a Simplified Quarter-Car Model" by Erik Mahieu.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send