Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Randomness Test in Coupon Collecting

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

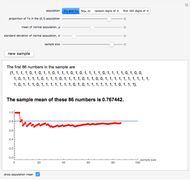
This is the coupon collector problem: suppose each package contains a coupon and that there are a certain number of different kinds of coupons. How many packages do you expect to have to open in order to form a complete collection?

[more]

The coupon collector randomness test is similar. For example, the packages are the digits of , and the coupons are the digits 0 to 9. How many digits do you expect to have to check before collecting all 10 digits?

This is the first coupon waiting time.

Repeat this process to obtain a sequence of coupon waiting times and compare the mean and distribution of these observed coupon waiting times to their theoretical mean and distribution.

This Demonstration illustrates the coupon collector problem randomness test for initial sequences of digits of famous irrational numbers and rational approximations of . The observed waiting time frequencies are given by the bar chart, and the theoretical frequencies are shown by the solid curve.

[less]

Contributed by: Tianli Li (May 2019)
Based on an undergraduate research project at the Illinois Geometry Lab by Raymond Harpster, Tianli Li and Yikai Teng and directed by A. J. Hildebrand.
Open content licensed under CC BY-NC-SA

Snapshots

Details

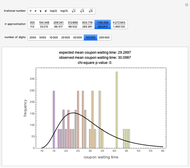
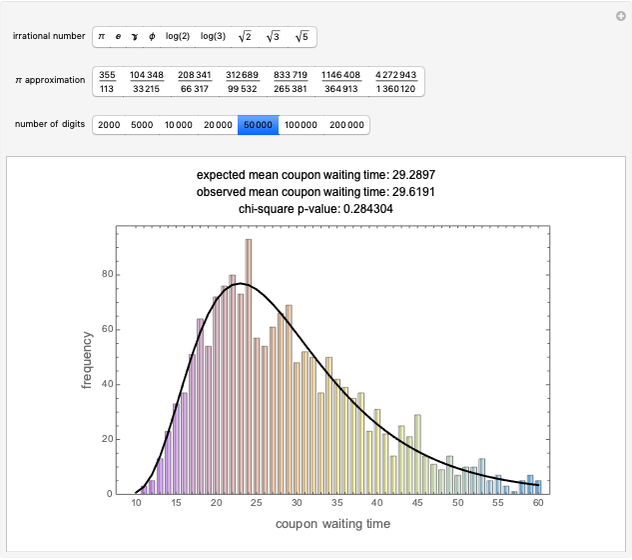
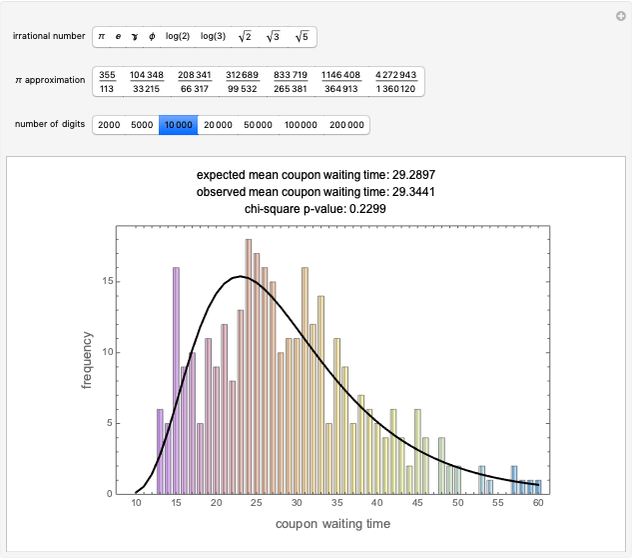
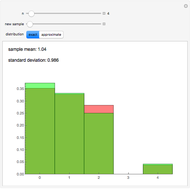
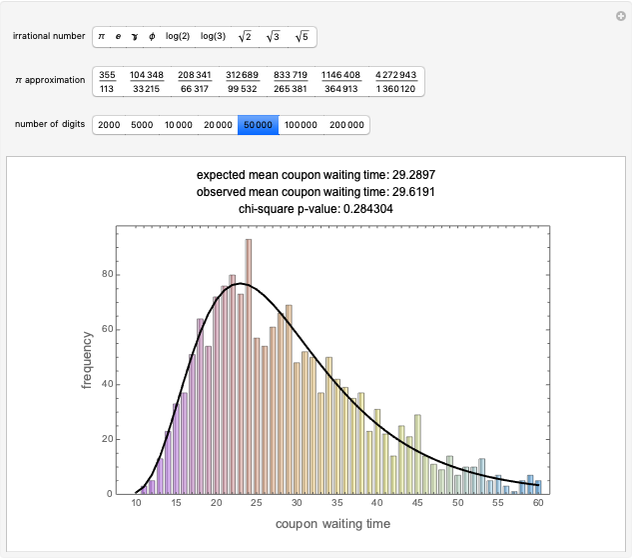
The expected waiting time in the coupon collector problem is given by , where is the number of coupons. For , this is . The theoretical distribution of these waiting times, the probabilities , where is the waiting time, is known and can be explicitly calculated as a finite sum.

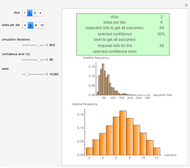
To compare the distribution of the theoretical and observed waiting times, apply the chi-squared test with five degrees of freedom after combining the observed waiting time counts into bins [10–19], [20–23], [24–27], [28–32], [33–39], [40–60]. The bins have been chosen to ensure approximately equal distribution of the waiting times.

References

[1] B. Dawkins, "Siobhan's Problem: The Coupon Collector Revisited," The American Statistician, 45(1), 1991 pp. 76–82. doi:10.1080/00031305.1991.10475772.

[2] R. E. Greenwood, "Coupon Collector’s Test for Random Digits," Mathematical Tables and Other Aids to Computation, 9(49), 1955 pp. 1–5. doi:10.2307/2002211.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send