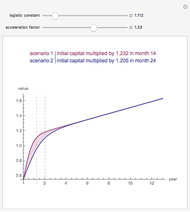
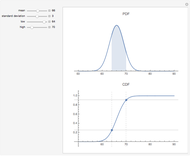
Granger-Orr Running Variance Test
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
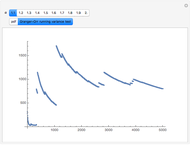
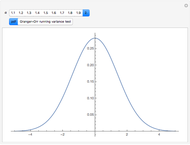
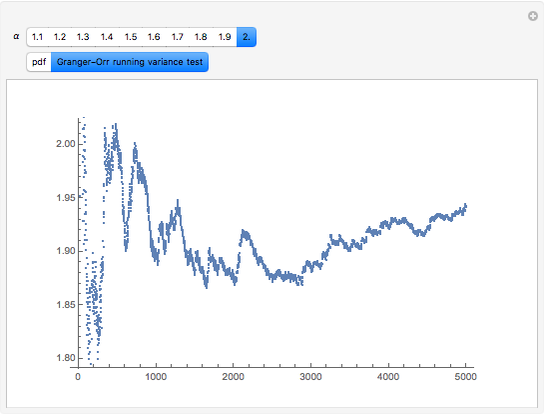
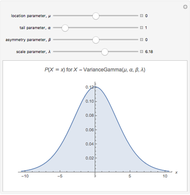
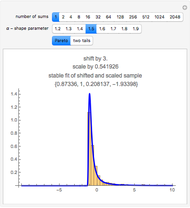
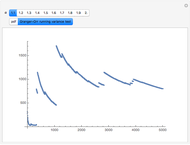
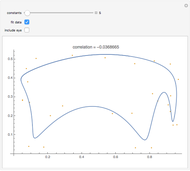
There is no test to prove a distribution is non-normal stable. However there are tests that indicate stability. One of these is a test for infinite variance. For the normal (a special case of stable) distribution the variance converges to a finite real number as 
grows without bounds. When tails are heavy (stable 
) variance does not exist or is infinite. Granger and Orr (1972) devised a running variance test for infinite variance that is displayed here.
Contributed by: Roger J. Brown (May 2009)
Reproduced by permission of Academic Press from Private Real Estate Investment ©2005
Open content licensed under CC BY-NC-SA
Snapshots
Details
The method of generating random variables used here is Chambers et al. Other approaches, based on their work, have been developed.
More information is available in chapter six of [3] and at mathestate.com.
References
[1] J. M. Chambers, C. L. Mallows, and B. W. Stuck, "A Method for Simulating Stable Random Variables," Journal of the American Statistical Association 71, 1976 pp. 1340–1344.
[2] C. W. J. Granger and D. Orr, "Infinite Variance and Research Strategy in Time Series Analysis," Journal of the American Statistical Association, 67(338), 1972 pp. 275-285.
[3] R. J. Brown, Private Real Estate Investment: Data Analysis and Decision Making, Burlington, MA: Elsevier Academic Press, 2005.
Permanent Citation
Predictive Scores and Ultimate Test Passage
Seth J. Chandler
Variance-Gamma Distribution
Peter Falloon
Variance-Bias Tradeoff
Ian McLeod
Comparing Two Means Using Independent Samples of Unknown Variance
Shailesh S. Kulkarni and Hakan Tarakci
Power Curve of a Mean Test
Sijia Liang and Bruce Atwood
One-Sample t-Test and Confidence Interval with Dot Chart in Small Samples
Douglas Woolford and Ian McLeod
Generalized Central Limit Theorem
Roger J. Brown and Bob Rimmer
Analysis of Diagnostic Accuracy Measures
Theodora Chatzimichail
Binomial Probability Distribution
Paul Savory (University of Nebraska ? Lincoln)
Intuitive Parameterization of the Bivariate Normal Distribution
Robert L. Brown
-
Dissolving Partnerships
Roger J. Brown -
Forming the Efficient Frontier When Returns Are Non-Normal
Roger J. Brown -
Spectral Measures
Roger J. Brown -
Granger-Orr Running Variance Test
Roger J. Brown -
Capitalization Rate Probability
Roger J. Brown -
Net Lease Economics
Roger J. Brown -
The Refinance Decision
Roger J. Brown -
True Cost of Variable Rate Mortgage Funds
Roger J. Brown -
Term Structure of Interest Rates
Roger J. Brown -
Generalized Central Limit Theorem
Roger J. Brown -
Inflation-Adjusted Yield
Roger J. Brown -
Simulating the IRR
Roger J. Brown -
Real Options
Roger J. Brown -
The Price-Terms Tradeoff
Roger J. Brown -
Fitting an Elephant
Roger J. Brown -
Solving the Subprime Loan Problem
Roger J. Brown -
Why Location Matters: The Bid Rent Curve
Roger J. Brown -
Explaining Real Estate Price Bubbles
Roger J. Brown -
Value Added Growth Model
Roger J. Brown -
Connecting the CDF and the PDF
Roger J. Brown