Sensitivity to Initial Conditions in Chaos

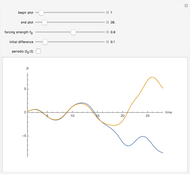
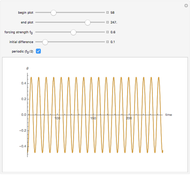
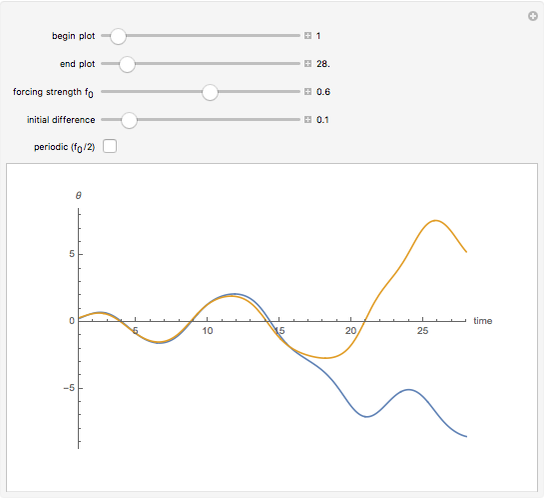
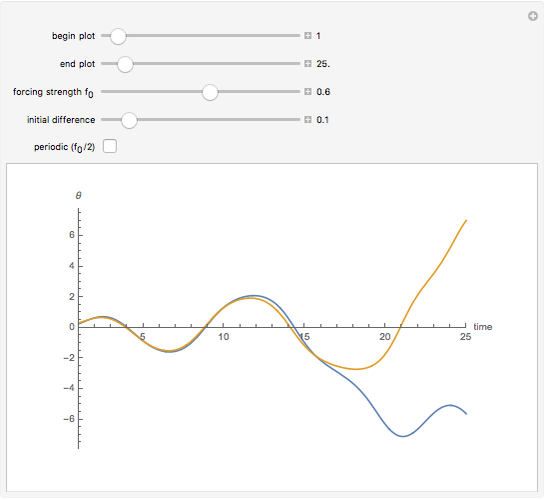
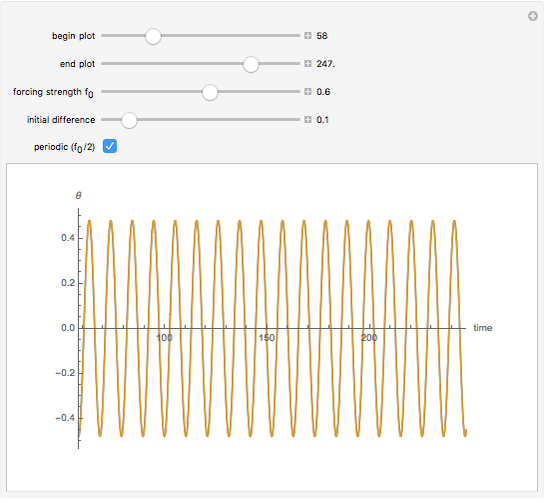
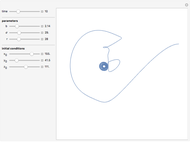
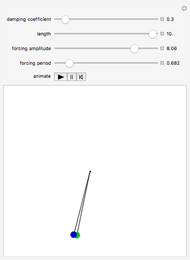
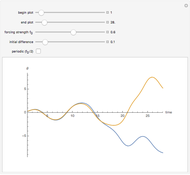
While there is no agreement on a definition of chaos, sensitivity to initial conditions is usually considered an important marker. This Demonstration compares plots of a driven pendulum in a chaotic regime, started at two slightly different positions, to the same pendulum restricted to a regime of periodic orbits. The periodic regime varies the periodic driving force amplitude from 0.05 to 0.5 instead of from 0.1 to 1.0. The larger range includes a number of periodic orbits as well as chaotic ones.