Solve the Cryptoquote Automatically

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
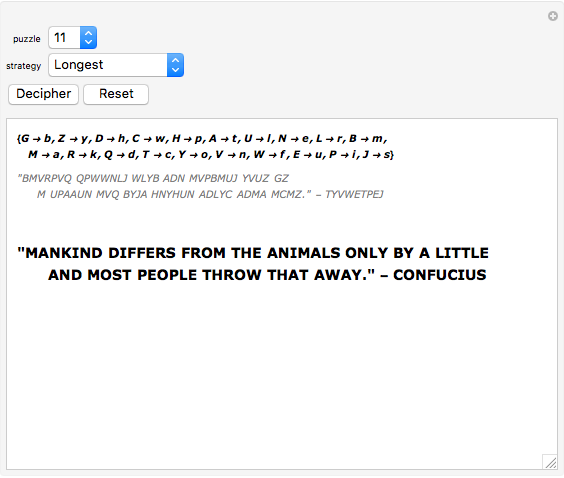
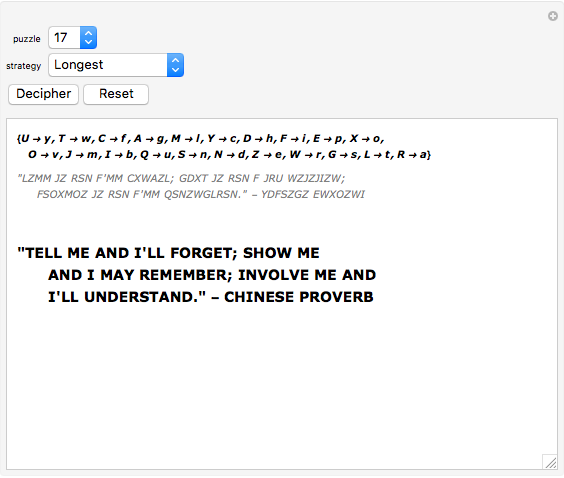
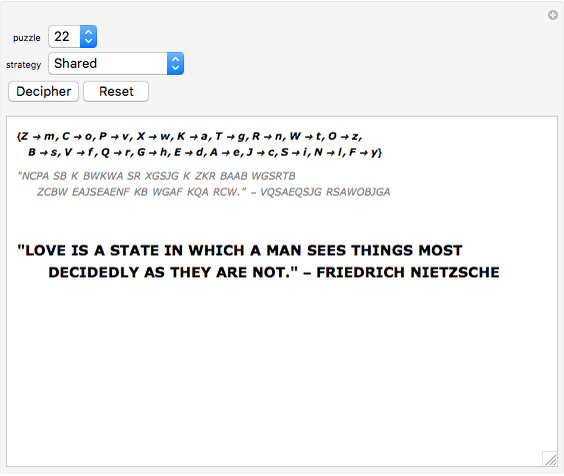
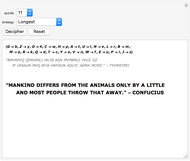
A cryptoquote is a puzzle, commonly found in newspapers, in which a substitution cipher is used to encrypt a famous quote. Here a brute force approach is taken to automatically decipher the encrypted text for 33 different puzzles listed in order of difficulty. The encrypted puzzle is dynamically updated as the solution progresses. Experiment with different solving strategies to enhance or degrade performance.
Contributed by: Andy Ross (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
A brute force approach will eventually solve any encrypted puzzle, but the practicality of such an approach is diminished by the staggering number of possibilities that must be tried. Human intuition allows us to solve these puzzles by using what we know about the structure of language to limit possibilities. A similar approach is taken here to make decryption reasonably fast.
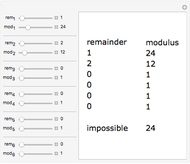
First, the puzzle is reduced to a list of words in their encrypted form. All characters are converted to uppercase letters that represent unknowns. Second, words are converted to string patterns so that Mathematica's DictionaryLookup function can be used to find candidate words for each pattern.
Once a list of candidate words has been created they can be used to form string replacement rules. It is assumed that a valid replacement rule is one-to-one, in the sense that one uppercase character maps to exactly one lowercase character and that no lowercase character is represented by more than one uppercase character.
A replacement rule is applied to the puzzle and the process repeats recursively, allowing the rule to grow as more characters become known. If a rule is applied and any of the unsolved words have no candidate solutions that rule is discarded. The puzzle is solved if all unknown characters have been replaced.
Since there is no practical way to check grammatical structure, only whether each word has been replaced by an English word, there are typically multiple solutions to the puzzle. The final solution that is presented is chosen by formulating scores for each candidate solution based upon letter frequency and common word prevalence. The frequency of letters in the English language are well known and are used here, for example. For common word comparison, the top 250 most common English words have been used with contractions removed.
In order to minimize the initialization but still arrive at correct solutions, the common word list has been augmented to include words such as "love", which is common in these puzzles, though the score associated with these added words has been kept as low as possible so as not to dramatically influence the process. Without adding those words, the solver may well prefer less common solutions. Take, for example, two solutions differing in one character with the words "love" and "lope". Obviously, "love" is the more common of the two; however, it is not sufficiently common to occur in the top 250 words and since "p" is more common than "v", the solution with "lope" would be chosen.
All solutions are arrived at for each puzzle rather than choosing the first one encountered. This means that a strategy must be employed to quickly remove impossible letter combinations. Here strategies determine the order in which words should be solved. The "Longest" strategy is typically the fastest and attempts to solve words by their length starting with the longest word. The "Shared" strategy attempts to solve words that share the most letters with the rest of the puzzle, which is also a very effective strategy.
The "WeightedShared" strategy applies weights to each character in the puzzle based on frequency and then computes a shared character score using these weights. This is typically most effective in puzzles that have a few very common characters. The "Shortest" strategy is the reverse of "Longest" and typically takes the most time to reach a solution. “Random” solves the words at random.
In general, this solver is most effective with longer puzzles containing longer words. The strategies employed here would be extremely fast at decrypting an entire book so long as all of its words are represented in the built-in dictionary. The methods used here could easily be extended to other languages by switching dictionaries. It would also be possible to improve things by using a longer list of common words. Note that once the solver has started it must be aborted with Alt + . in order to halt its progress. The "Reset" button will remove the current rule and return the puzzle back to its unsolved form.
Permanent Citation
"Solve the Cryptoquote Automatically"
http://demonstrations.wolfram.com/SolveTheCryptoquoteAutomatically/
Wolfram Demonstrations Project
Published: March 7 2011