Stability of Polygons Inscribed in an Ellipse

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
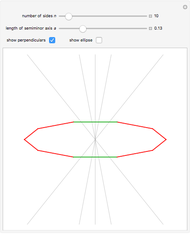
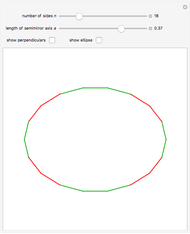
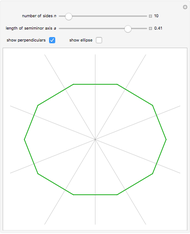
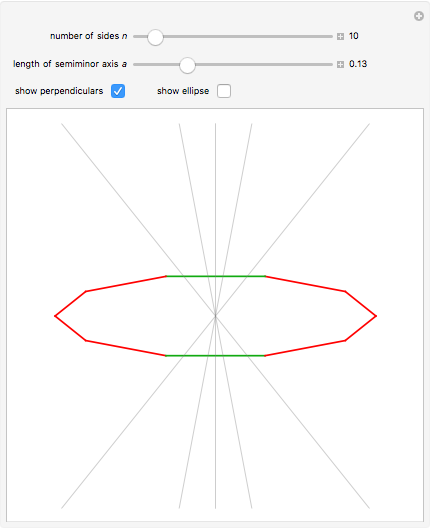
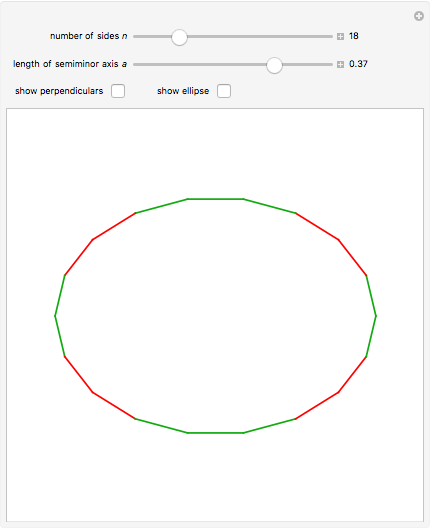
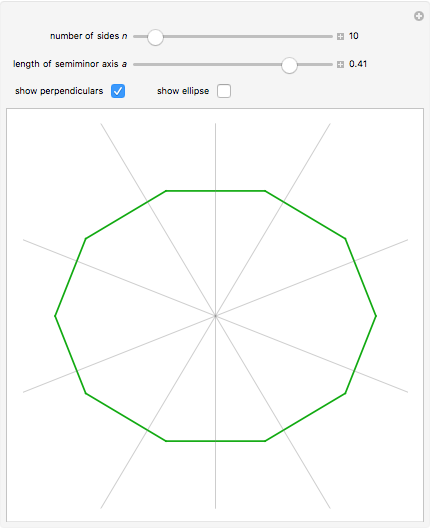
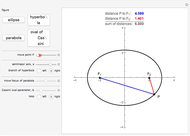
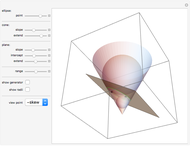
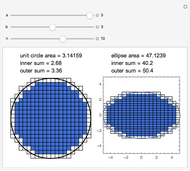
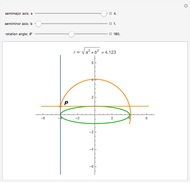
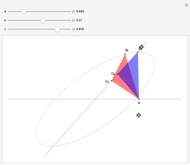
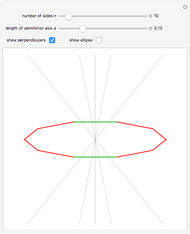
This Demonstration concerns polygons with  sides inscribed in an ellipse with semimajor axis 1 and semiminor axis
sides inscribed in an ellipse with semimajor axis 1 and semiminor axis  . If there exists a perpendicular line from a side that intersects the center of gravity, then the side is stable. The stable sides are shown in green.
. If there exists a perpendicular line from a side that intersects the center of gravity, then the side is stable. The stable sides are shown in green.
Contributed by: Tímea Deichler (June 2015)
Suggested by: Gabor Domokos
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] G. Domokos, Z. Lángi, and T. Szabó, "On the Equilibria of Finely Discretized Curves and Surfaces," Monatshefte für Mathematik, 168(3–4), 2012 pp. 321–345.
[2] "The Gömböc." (Jun 25, 2015) www.gomboc.eu.
Permanent Citation