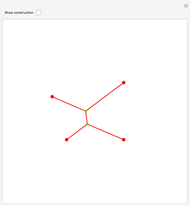
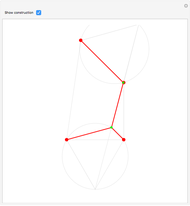
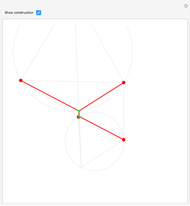
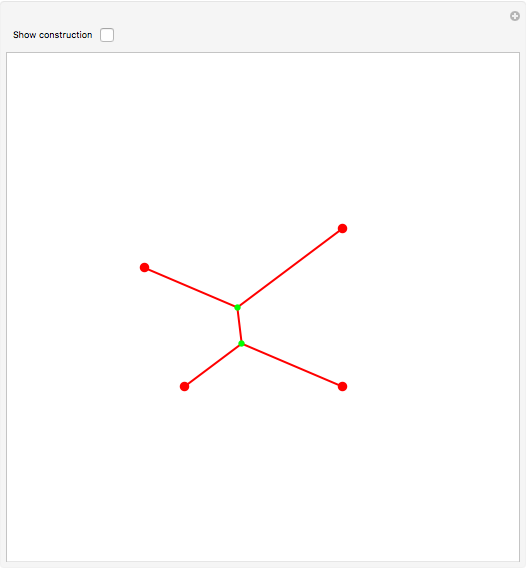
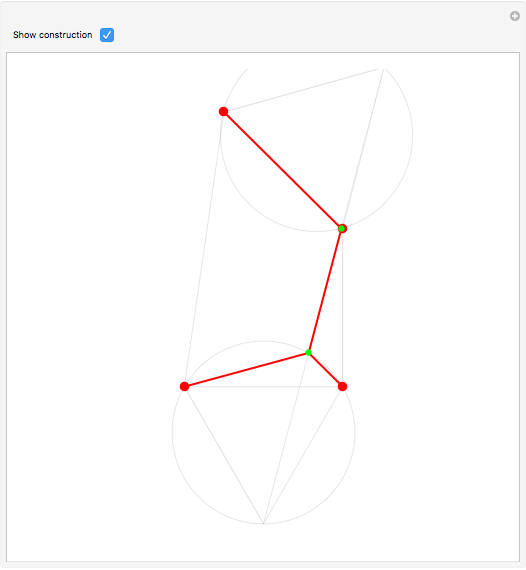
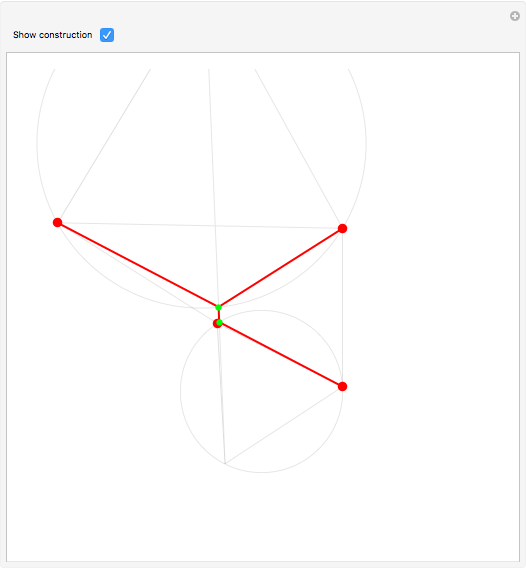
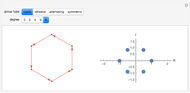
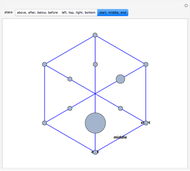
Steiner Networks for Four Points

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
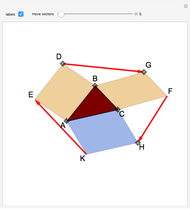
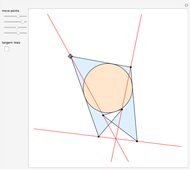
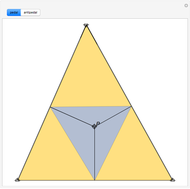
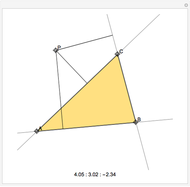
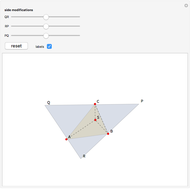
The Fermat (or Torricelli) point  of a triangle minimizes the sum of the distances from
of a triangle minimizes the sum of the distances from  to each of the vertices.
to each of the vertices.
Contributed by: Jaime Rangel-Mondragon (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
D. Wells, The Penguin Dictionary of Curious and Interesting Geometry, London: Penguin, 1992.
Permanent Citation
"Steiner Networks for Four Points"
http://demonstrations.wolfram.com/SteinerNetworksForFourPoints/
Wolfram Demonstrations Project
Published: March 7 2011