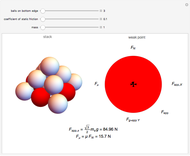
Structural Analysis of a Pyramid

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
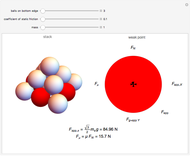
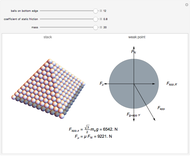
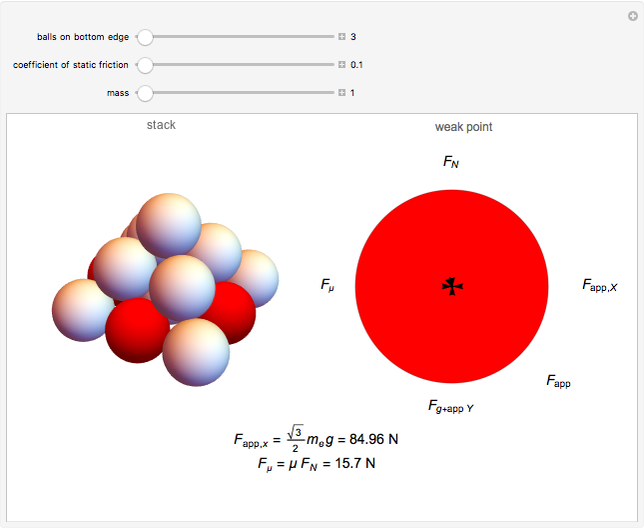
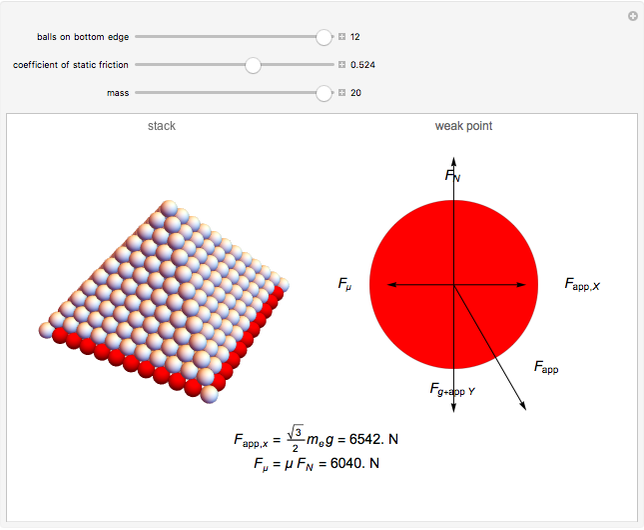
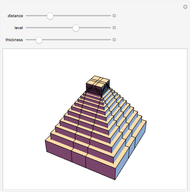
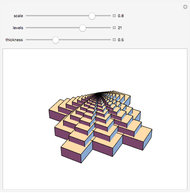
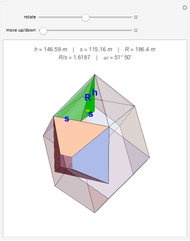
A pyramid with a square base of identical spheres fails structurally for certain coefficients of static friction for the stacking surface. As the number and mass of the balls increase, the mass of the pyramid applies an increasing force  to each ball on the bottom layer. This force eventually exceeds the capacity of the frictional force, which is limited by the coefficient of static friction
to each ball on the bottom layer. This force eventually exceeds the capacity of the frictional force, which is limited by the coefficient of static friction  between the floor and the balls. The first points of failure are the balls along the perimeter of the base, excluding the corners; these balls are colored red but change to gray when the component of
between the floor and the balls. The first points of failure are the balls along the perimeter of the base, excluding the corners; these balls are colored red but change to gray when the component of  that is parallel to the floor exceeds the capacity of the frictional force.
that is parallel to the floor exceeds the capacity of the frictional force.
Contributed by: Meera Desai (July 2013)
(Mathematica Summer Camp 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
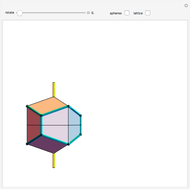
Each red ball supports two balls from the layer above. Each of the balls on the upper layer have the same effective mass  , and therefore apply the same force to the balls supporting them. The effective mass of each ball is calculated by separating the base layer from the remaining smaller pyramid. Multiplying the number of balls in the smaller pyramid by the mass of each ball gives the total mass of the smaller pyramid. This mass is distributed evenly over a certain number of points of contact with the base layer. Each ball in the base of the smaller pyramid contacts the base layer in four places. Dividing the number of contact points between a given ball and the smaller pyramid by the total number of contact points creates a ratio. When this ratio is multiplied by the total mass of the smaller pyramid, the effective mass of a specific ball can be calculated. The corners of the pyramid have a lower value for
, and therefore apply the same force to the balls supporting them. The effective mass of each ball is calculated by separating the base layer from the remaining smaller pyramid. Multiplying the number of balls in the smaller pyramid by the mass of each ball gives the total mass of the smaller pyramid. This mass is distributed evenly over a certain number of points of contact with the base layer. Each ball in the base of the smaller pyramid contacts the base layer in four places. Dividing the number of contact points between a given ball and the smaller pyramid by the total number of contact points creates a ratio. When this ratio is multiplied by the total mass of the smaller pyramid, the effective mass of a specific ball can be calculated. The corners of the pyramid have a lower value for  , because the corner balls support only one ball, instead of two.
, because the corner balls support only one ball, instead of two.
 is the force exerted on a single ball in the perimeter of the base layer (excluding corners) by the two balls it supports. Because there are two balls and the force comes in at a
is the force exerted on a single ball in the perimeter of the base layer (excluding corners) by the two balls it supports. Because there are two balls and the force comes in at a  angle from the vertical (clear from the symmetry of the pyramid), multiplying
angle from the vertical (clear from the symmetry of the pyramid), multiplying  gives the value for
gives the value for  at
at  from the vertical. The component of
from the vertical. The component of  that is parallel to the floor opposes the force of friction
that is parallel to the floor opposes the force of friction  . This component of
. This component of  can be expressed as
can be expressed as  . When F μ<
. When F μ< , the pyramid falls.
, the pyramid falls.
Interestingly, the mass of each ball does not have an effect on the structural integrity of a pyramid with identical balls. When the mass of the pyramid increases, so does the force of gravity  . Because the sum of the forces in the direction perpendicular to the floor is always zero, when
. Because the sum of the forces in the direction perpendicular to the floor is always zero, when  increases,
increases,  must also increase to compensate.
must also increase to compensate.  , so when
, so when  increases, so does
increases, so does  .
.
Permanent Citation