The 14 3D Bravais Lattices

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
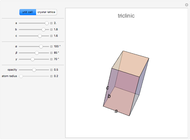
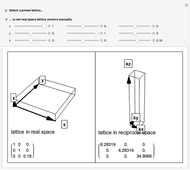
This Demonstration shows the characteristics of 3D Bravais lattices arranged according to seven crystal systems: cubic, tetragonal, orthorhombic, monoclinic, triclinic, rhombohedral and hexagonal. Each crystal system can be further associated with between one and four lattices by adding to the primitive cell (click "P"): a point in the center of the cell volume (click "I"), a point at the center of each face (click "F") or a point just at the center of the base faces (click "C"). The points located at the center/faces are highlighted in blue; each point is also a vertex or center of the cell/face, therefore each point is equivalent to every other point.
[more]
Contributed by: D. Meliga and S. Z. Lavagnino (September 2016)
With additional contribution by: G. Follo
Open content licensed under CC BY-NC-SA
Details
The Bravais lattice theory establishes that crystal structures can be generated starting from a primitive cell and translating along integer multiples of its basis vectors, in all directions.
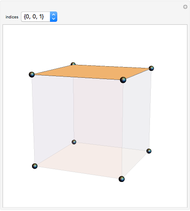
Snapshot 1: This shows the primitive cubic system consisting of one lattice point at each corner of the cube. Each atom at a lattice point is then shared equally between eight adjacent cubes, and the unit cell therefore contains in total one atom  . The crystal structure of pyrite
. The crystal structure of pyrite  is primitive cubic [2].
is primitive cubic [2].
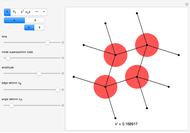
Snapshot 2: The face-centered cubic system has lattice points on the faces of the cube; each contributes exactly  , in addition to the corner lattice points, giving a total of four lattice points per unit cell (
, in addition to the corner lattice points, giving a total of four lattice points per unit cell ( from the corners plus
from the corners plus  from the faces). The crystal structure of sodium chloride
from the faces). The crystal structure of sodium chloride  is face-centered cubic [2].
is face-centered cubic [2].
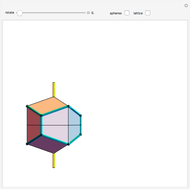
Snapshot 3: This shows the hexagonal system. Graphite is an example of the hexagonal crystal system [2].
References
[1] M. de Graef and M. E. McHenry, Structure of Materials: An Introduction to Crystallography, Diffraction and Symmetry, Cambridge: Cambridge University Press, 2007.
[2] W. B. Pearson, A Handbook of Lattice Spacings and Structures of Metals and Alloys, New York: Pergamon Press, 1958.
Snapshots
Permanent Citation