Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

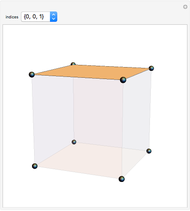
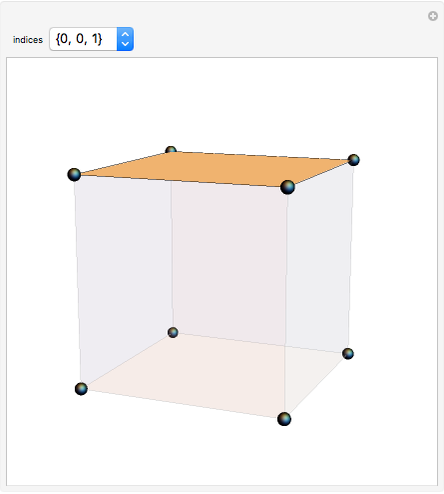
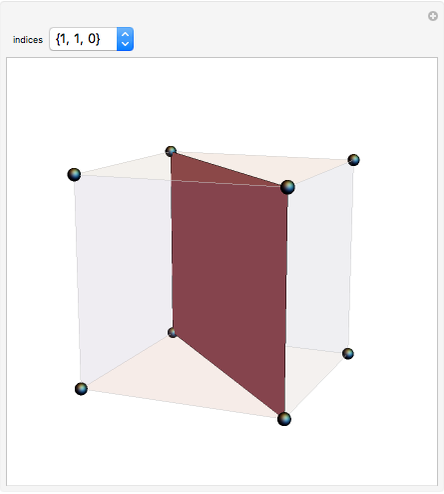
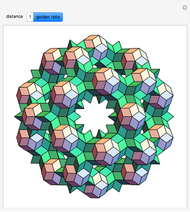
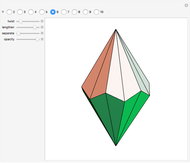
Miller Indices for a Simple Cubic Lattice

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

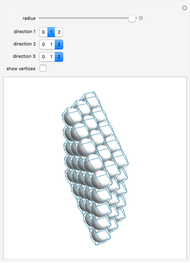
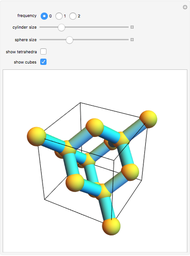
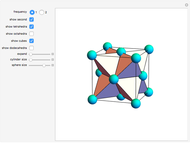
Miller indices are a notation to identify planes in a crystal. The three integers 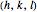define directions orthogonal to the planes, thus constituting reciprocal basis vectors. Negative integers are usually written with an overbar (e.g., represents ).

[more]

The nine lowest-index planes are shown.

[less]

Contributed by: Enrique Zeleny (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

detailSectionParagraph
Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send