The Euclidean Algorithm and Simple Continued Fractions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
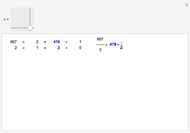
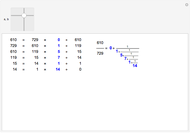
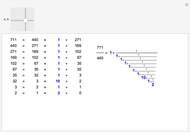
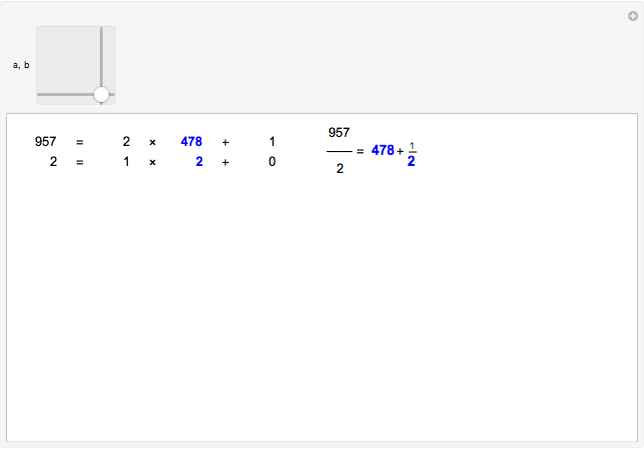
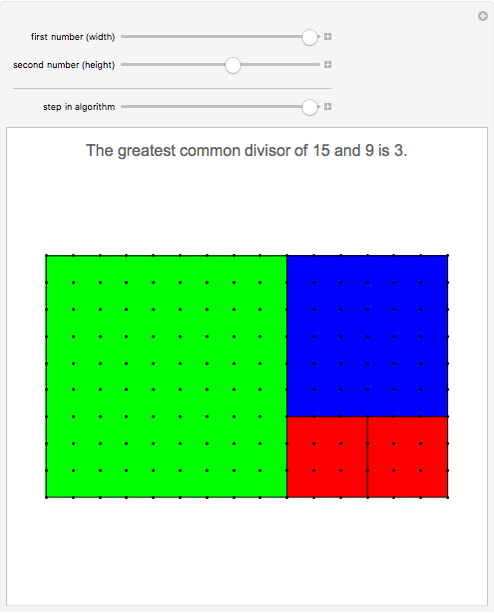
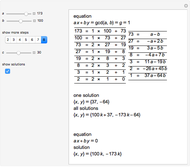
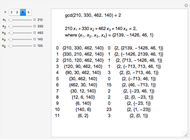
This Demonstration shows the connection between the continued fraction expansion of a rational number 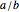 and the Euclidean algorithm applied to the pair of integers
and the Euclidean algorithm applied to the pair of integers  and
and  .
.
Contributed by: Štefan Porubský (June 2008)
Based on a program by: Michael Trott
Open content licensed under CC BY-NC-SA
Snapshots
Details
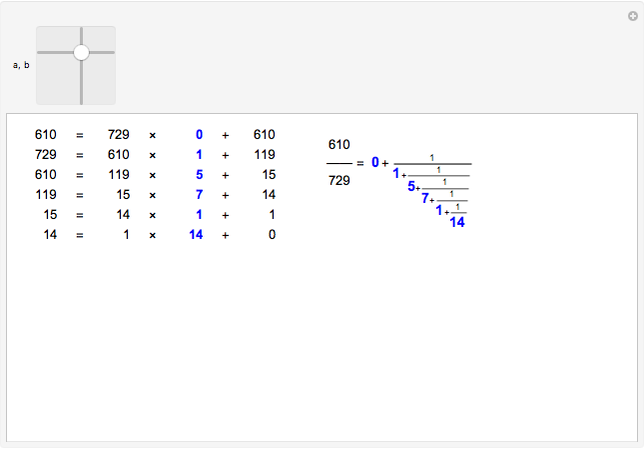
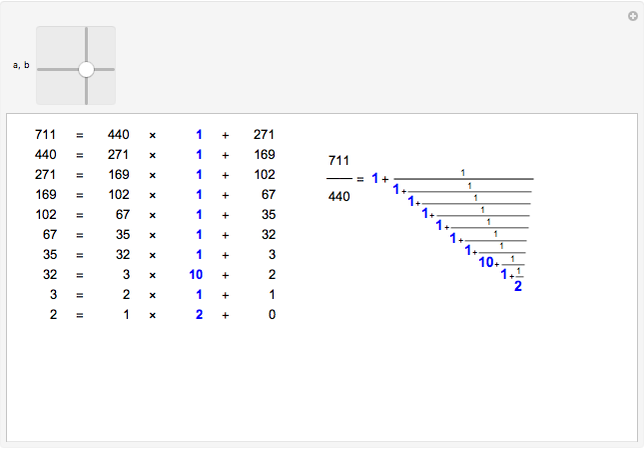
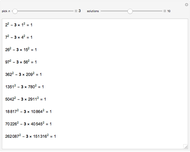
The simple continued fraction expansion of a real number  is finite if and only if
is finite if and only if  is rational. The process of finding the simple continued fraction expansion of a rational number is in principle identical to the process of applying the Euclidean algorithm to its numerator and denominator. For example,
is rational. The process of finding the simple continued fraction expansion of a rational number is in principle identical to the process of applying the Euclidean algorithm to its numerator and denominator. For example,
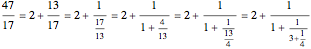 .
.
The underlying Mathematica program is an adaptation of the one used in The Wolfram Demonstration Projects Euclidean Algorithm Steps by Michael Trott and Extended Euclidean Algorithm by Štefan Porubský.
(The author was supported by project 1ET200300529 of the program Information Society of the National Research Program of the Czech Republic and by the Institutional Research Plan AV0Z10300504; the Demonstration was submitted 2008-06-04, revised 2010-03-13.)
Permanent Citation