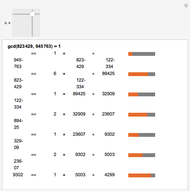
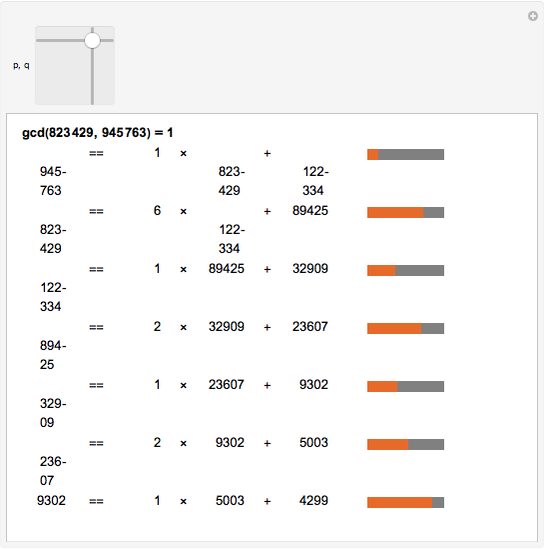
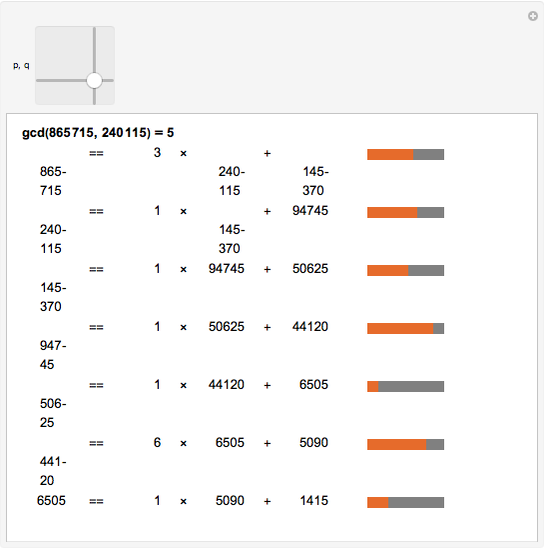
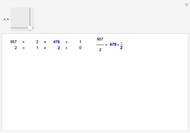
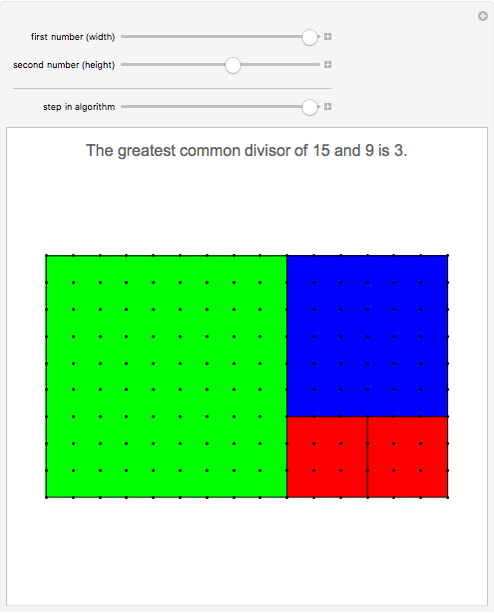
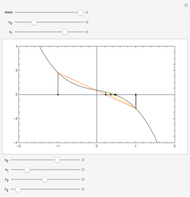
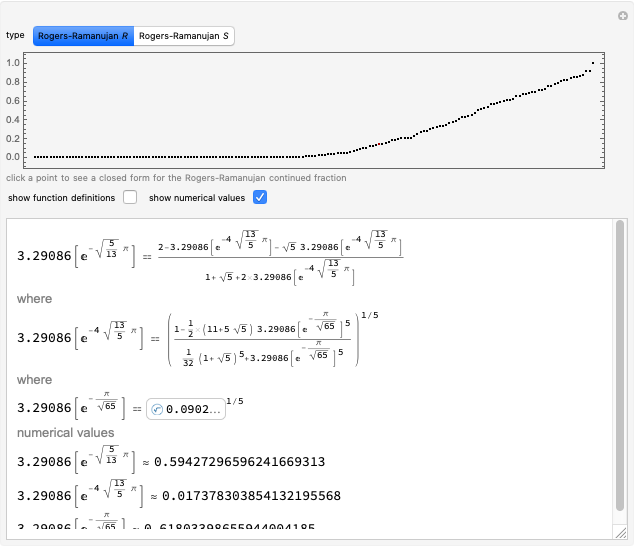
The steps in the Euclidean algorithm, which calculates the greatest common divisor of two positive integers. The red bars indicate the fraction of the remainder to the divisor.
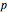, — pair of integers whose greatest common divisor is to be calculated.
Algorithms are becoming more and more important. Nearly everyone encounters the PAGERANK algorithm (from Mr. Page) every day. One of the first (and still one of the most beautiful and useful) algorithms is the 2300-year-old Euclidean algorithm that calculates the greatest common divisor of two positive integers. Don Knuth once said that computer science will become a science when it has made 1000 algorithms. This Demonstration shows how it all got started. Can you find the pair of numbers that generate the longest output? (Hint: rabbits.)
Browse all topics
