The Four Numbers Game

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
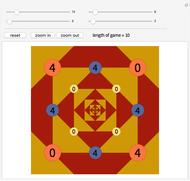
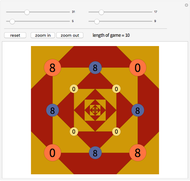
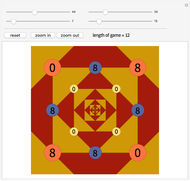
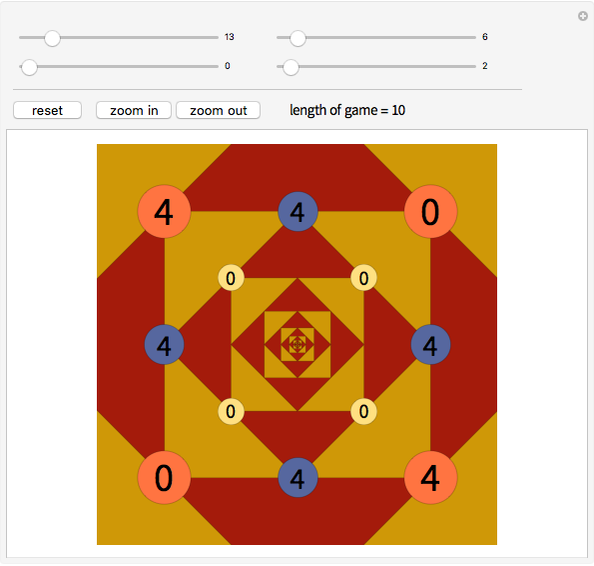
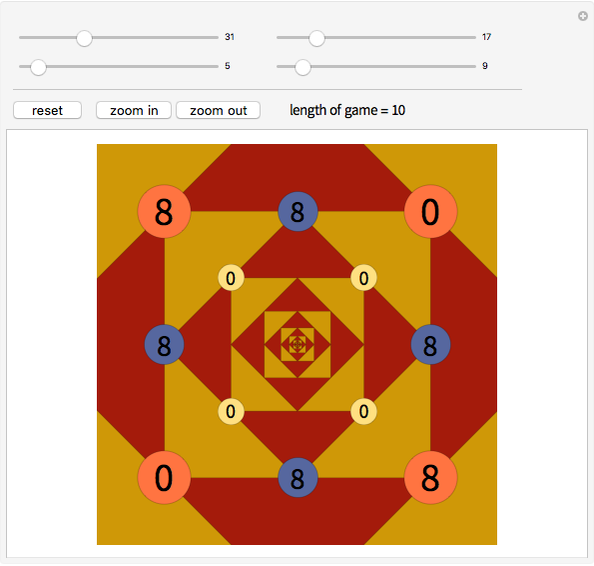
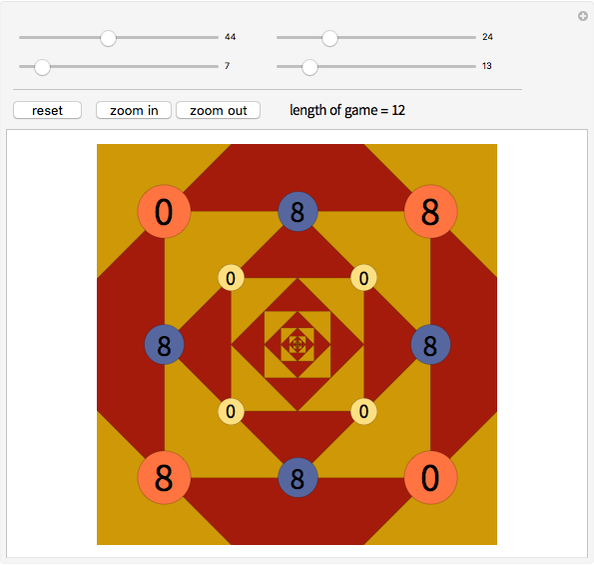
The Four Numbers Game is played starting with four non-negative integers (not necessarily different) placed at the vertices of a square (shown on orange disks above).
[more]
Contributed by: Jaime Rangel-Mondragon (August 2012)
Suggested by: Sol Lederman
Open content licensed under CC BY-NC-SA
Snapshots
Details
It is easy to see that the length of a game does not change if the initial configuration of numbers is rotated or reflected (eight possibilities in total); the length of the game is invariant under the symmetries of the square. One may wonder whether every game ends. The answer is affirmative; more precisely, if  is the largest of the four non-negative integers we start with and
is the largest of the four non-negative integers we start with and  is the least integer such that
is the least integer such that  , then the length of the game is at most
, then the length of the game is at most 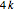 . For example, if
. For example, if  then
then  and the game lasts at most 44 steps.
and the game lasts at most 44 steps.
For every positive integer  , there is a game of length
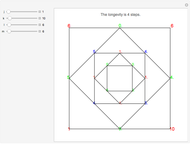
, there is a game of length  . Most games are of length 4 or 6;
. Most games are of length 4 or 6; 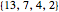 is of length 9. If we play with non-negative real numbers, some games have finite length; for instance,
is of length 9. If we play with non-negative real numbers, some games have finite length; for instance, 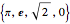 has finite length.
has finite length.
Reference
[1] J. D. Sally and P. J. Sally Jr., Roots to Research: A Vertical Development of Mathematical Problems, Providence, RI: American Mathematical Society, 2007.
Permanent Citation