The Great Brachistochrone Race

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
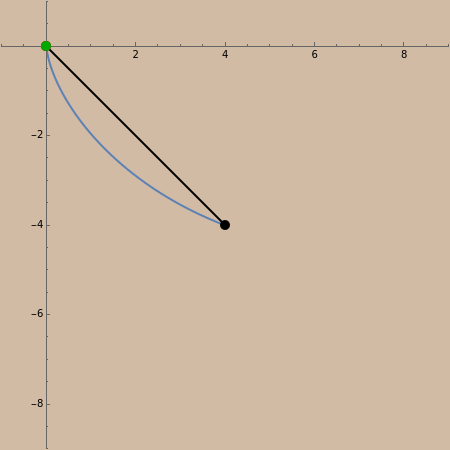
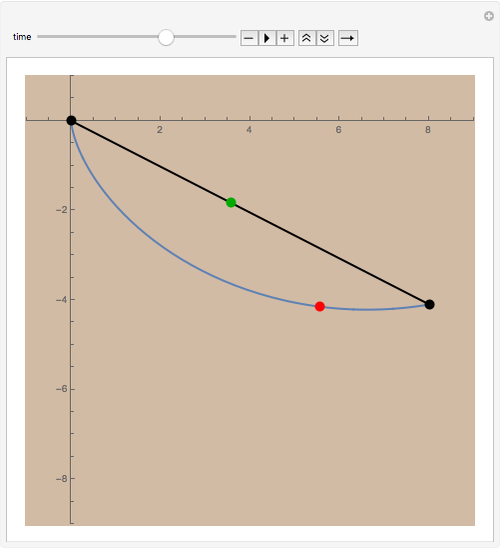
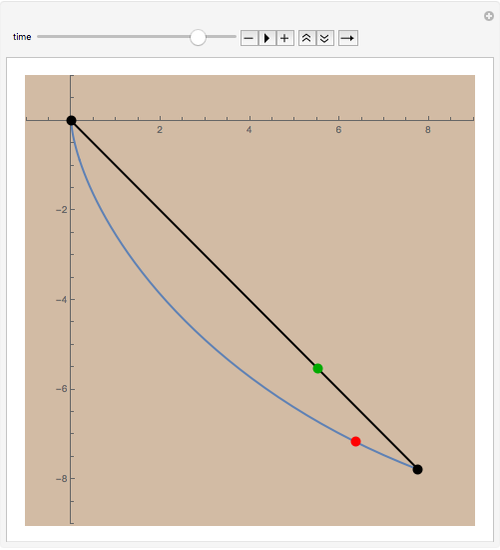
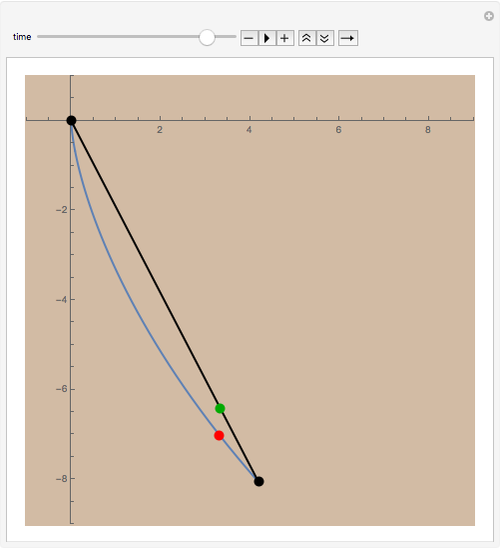
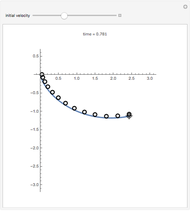
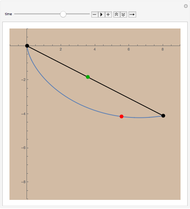
Construct a smooth slide so that a particle can descend from one point to another positioned below it (but not directly below). The classic brachistochrone problem: what form should the slide take to minimize the time of descent?
[more]
Contributed by: Phil Ramsden (May 2015)
Open content licensed under CC BY-NC-SA
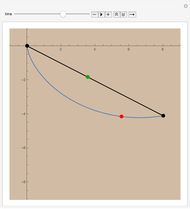
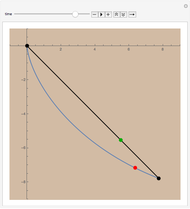
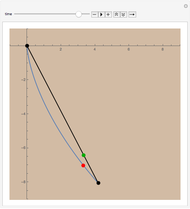
Snapshots
Details
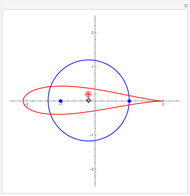
An arc of a cycloid has parametric equations  ,
,  . The value of
. The value of  is calculated (usually numerically, as it is in this Demonstration) so that the cycloid passes through the lower point for some value of
is calculated (usually numerically, as it is in this Demonstration) so that the cycloid passes through the lower point for some value of  between
between  and
and  .
.
The cycloid may be derived by using the techniques of variational calculus to find that function  of
of  that minimizes the integral
that minimizes the integral  along the curve (where
along the curve (where  is the differential of arc length).
is the differential of arc length).
When the value of the scaling constant  has been calculated, the parameter
has been calculated, the parameter  is found to be linearly related to the time
is found to be linearly related to the time  by the equation
by the equation  .
.
In this Demonstration, you can drag the lower point freely in the fourth quadrant of the  -
- plane, and you can animate the race down between a point on the straight line and a point on the cycloid.
plane, and you can animate the race down between a point on the straight line and a point on the cycloid.
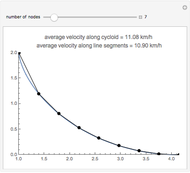
The cycloid always wins, but its winning margin depends on the steepness of the descent. For shallow descents, the cycloid's advantage is clear and enormous; for steep ones, the result is closer to a photo finish.
The animation rate has been scaled so that the value of  appears to be the same for all choices of the lower point.
appears to be the same for all choices of the lower point.
Permanent Citation