Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Conic Sections: The Double Cone

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

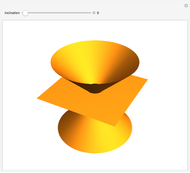
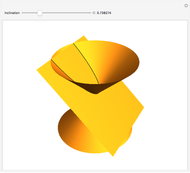
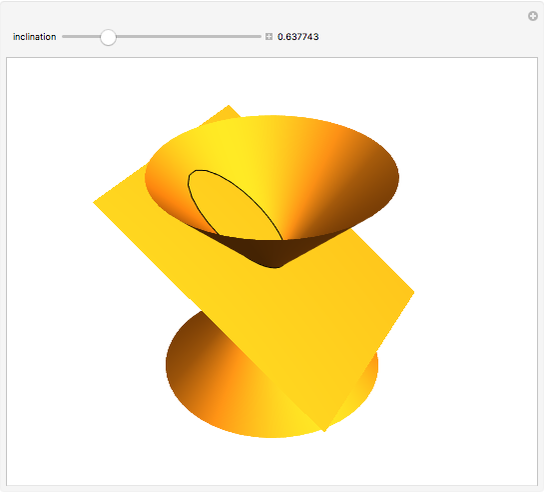
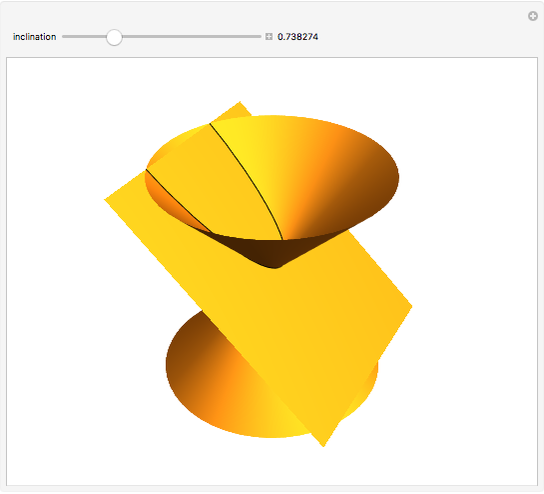
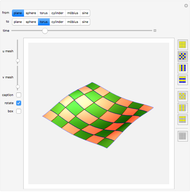
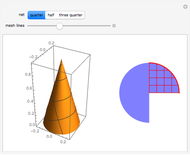
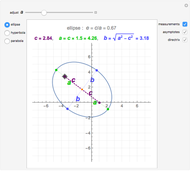
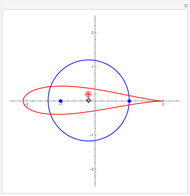
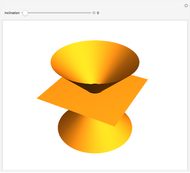
The quadratic curves are circles, ellipses, parabolas, and hyperbolas. They are called conic sections because each one is the intersection of a double cone and an inclined plane. If the plane is perpendicular to the cone's axis, the intersection is a circle. If it is inclined at an angle greater than zero but less than the half-angle of the cone, it is an (eccentric) ellipse. If the plane's inclination is equal to this half-angle, the intersection is a parabola. If it exceeds the half-angle, it is a hyperbola.

[more]

When the plane passes through the apex of the cone, the intersection is a point, one line, or a double line.

[less]

Contributed by: Phil Ramsden (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Mathematical note: If the half-angle of the cone is 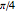then the eccentricity of the intersection is 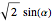, where is the angle of inclination of the plane. Its projection in the 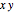plane is also a conic section, with focus at the origin and eccentricity 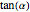. Note that the eccentricity of the intersection and of its projection are equal for precisely two values of , namely 0 and 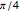, corresponding to eccentricities of 0 and 1, and thus to the circle and parabola, respectively.

Snapshot 1: circle

Snapshot 2: ellipse

Snapshot 3: parabola

Snapshot 4: hyperbola

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send