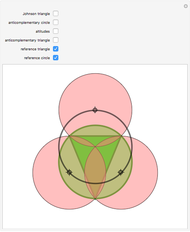
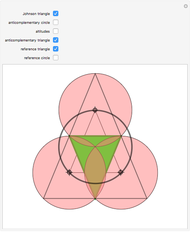
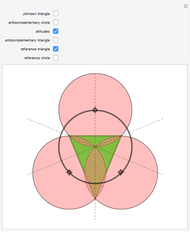
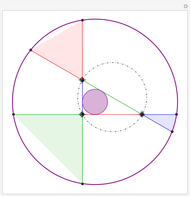
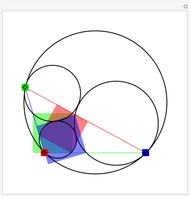
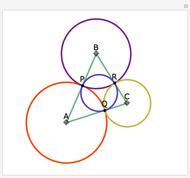
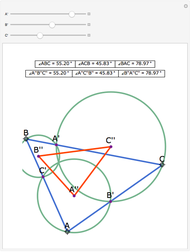
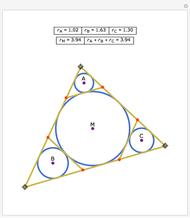
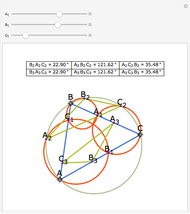
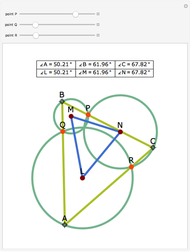
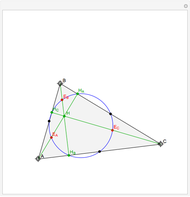
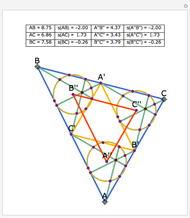
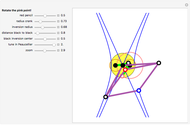
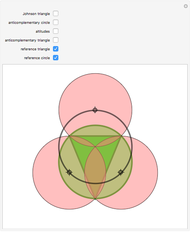
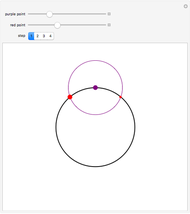
The Johnson Circles

The Johnson circles are a triplet of congruent circles sharing a single point. Every triangle has exactly two Johnson triplets.

Properties:

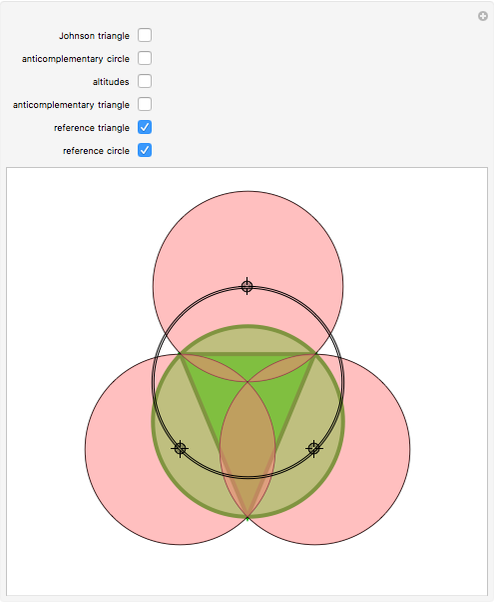
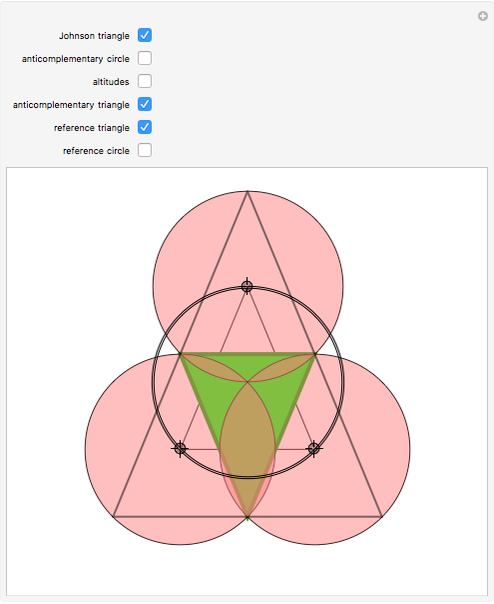
• The locators are the centers of the three circles. They form the Johnson triangle with circumcircle of the same radius.

• Johnson's theorem: the "reference triangle" with vertices the points of two-fold intersection has, surprisingly, a circumcircle of the same radius.

• The reference triangle is congruent to the Johnson triangle by homothety of factor .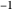

• The anticomplementary circle with twice the radius touches the Johnson circles.

• The inscribed anticomplementary triangle is homothetic to the Johnson triangle with factor 2.

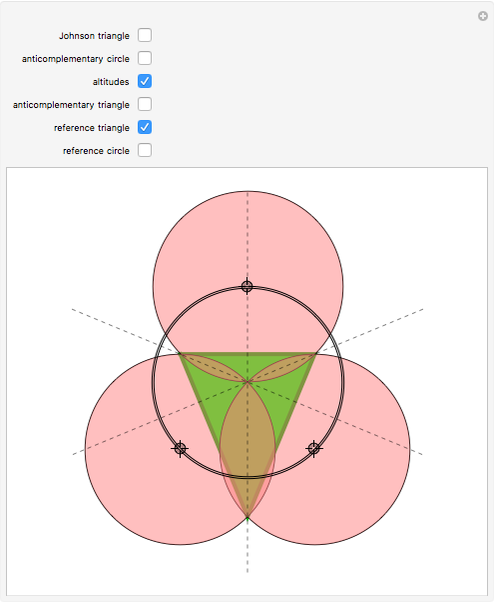
• The three locators and the origin are, surprisingly, such that each is the orthocenter of the three others.

• The homothetic center of the Johnson and reference triangle is the center of the nine-point circle of the reference triangle.