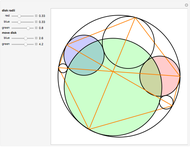
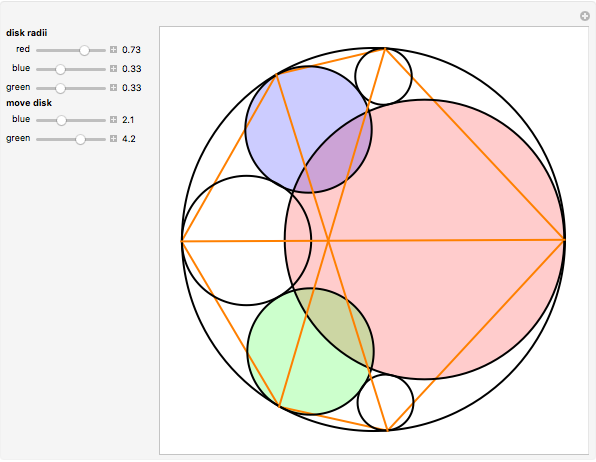
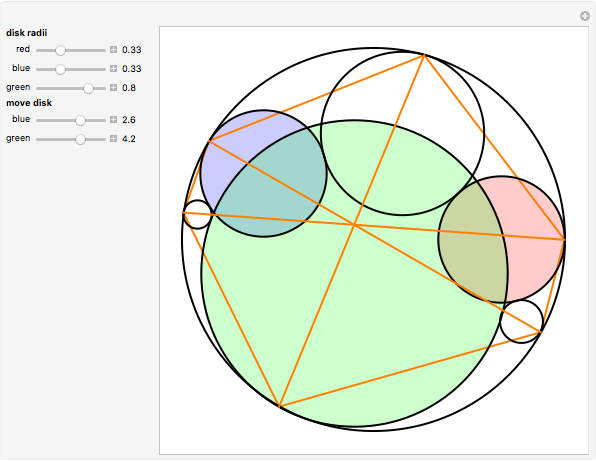
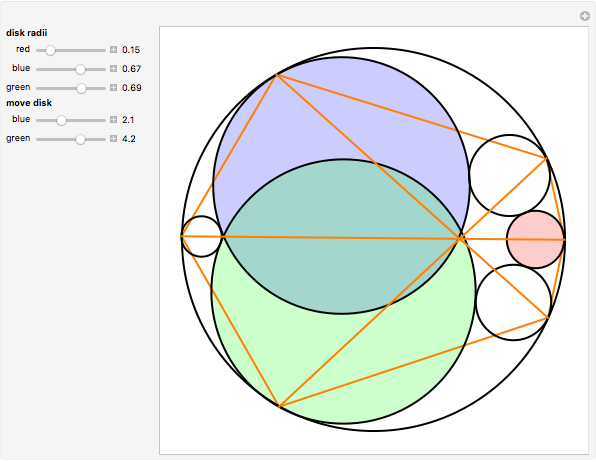
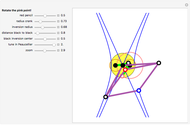
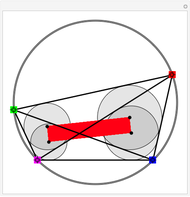
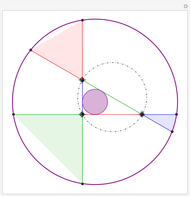
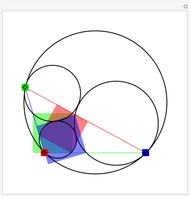
Take six circles tangent to each other in pairs and tangent to the unit circle on the inside. The points of contact of the six circles with the unit circle define a hexagon. The diagonals of the hexagon are concurrent.
This concurrency is obvious when the hexagon is regular. The theorem states that it still holds when the radii and the positions of the circles vary.
This remarkable theorem is quite young. Evelyn, Money-Coutts, and Tyrrell first published it in 1974. The reason for this late discovery could be the difficulty of constructing a circle tangent to three other circles (Apollonius's problem). No practicable way has been found using straightedge and compass.
Mathematica readily solves three simultaneous quadratic equations to determine the tangent circle.
The conclusion also holds when the six circles are tangent to the unit circle from the outside.
![[Snapshot]](HTMLImages/index.en/thumbnail_1.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_2.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_3.gif)
Browse all topics
