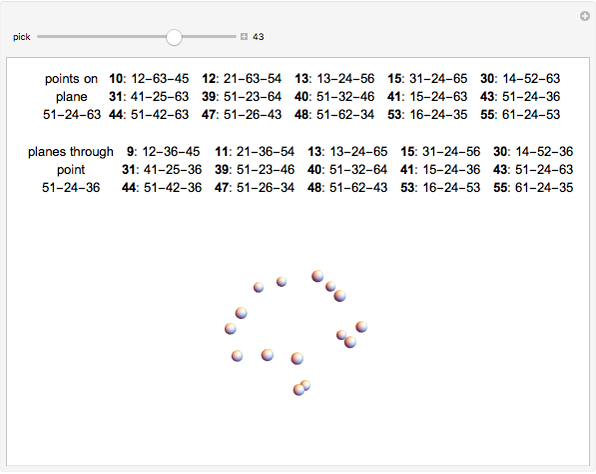
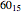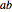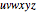The Klein Configuration

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Take three points  ,
, 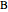 ,
,  on one line and three points
on one line and three points  ,
,  ,
,  on another line. Join them with six lines and define three points
on another line. Join them with six lines and define three points 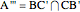 ,
,  ,
,  . Pappus's theorem states that
. Pappus's theorem states that  ,
, 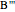 ,
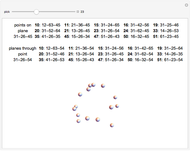
,  lie on a line. These nine points and nine lines represent a "configuration". Each point is on three lines, and each line goes through three points. This is called the Pappus
lie on a line. These nine points and nine lines represent a "configuration". Each point is on three lines, and each line goes through three points. This is called the Pappus  configuration.
configuration.
Contributed by: Ed Pegg Jr (November 2016)
Open content licensed under CC BY-NC-SA
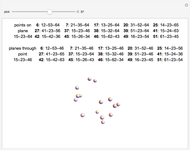
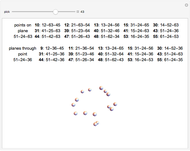
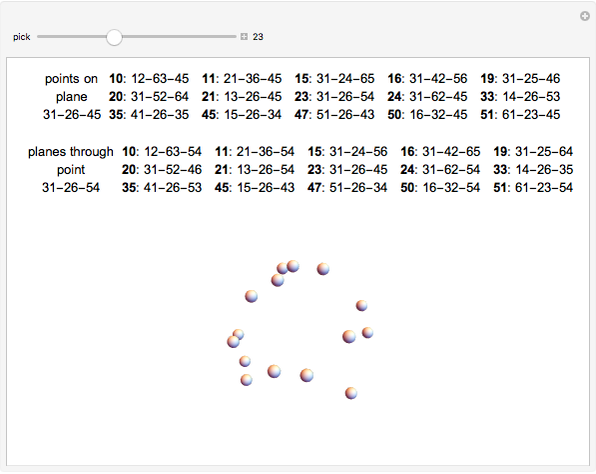
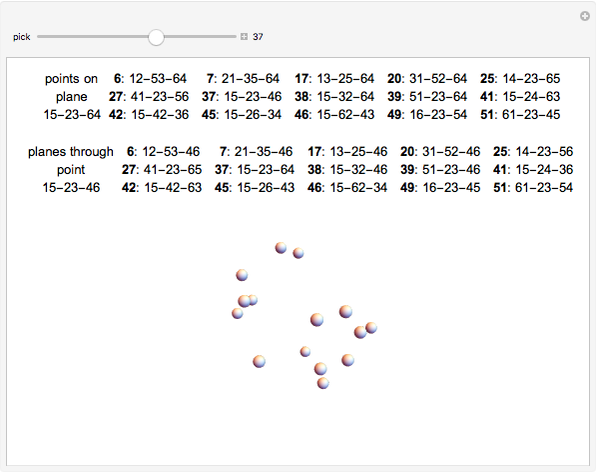
Snapshots
Details
Further details are in [1].
Reference
[1] R. W. H. T. Hudson, Kummer's Quartic Surface, 1905. archive.org/details/quarticsurface00kummrich.
Permanent Citation