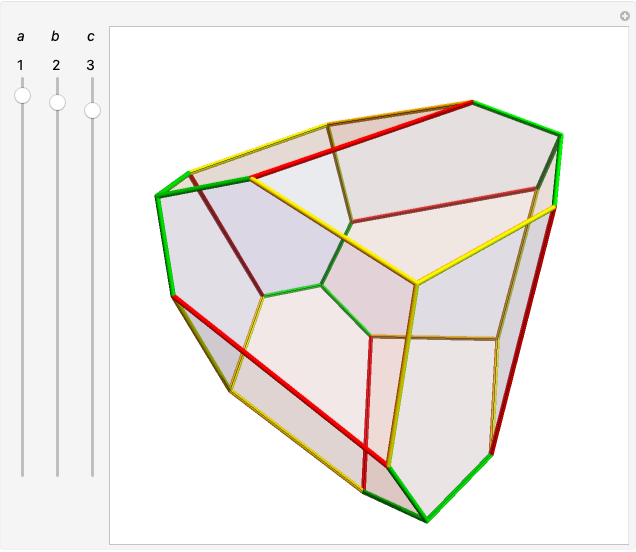
Biggest Little Polyhedron

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
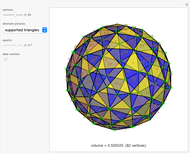
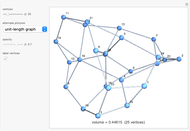
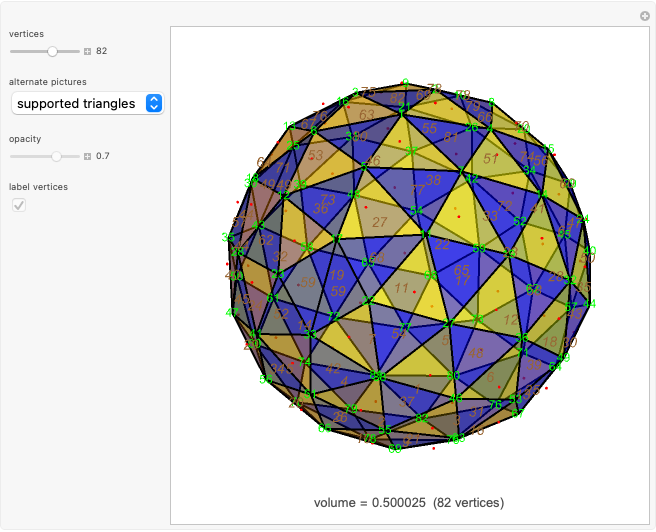
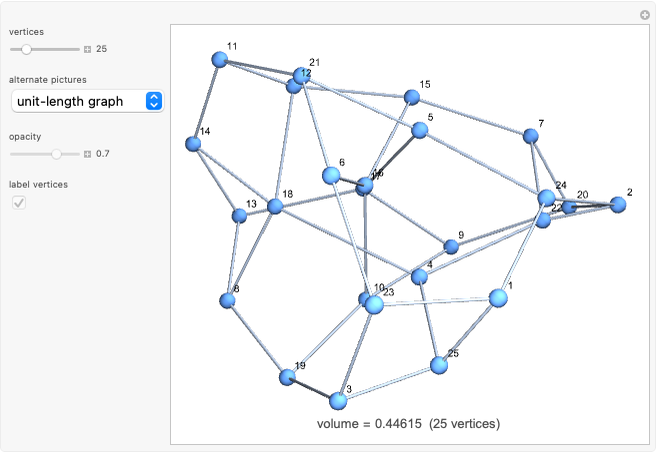
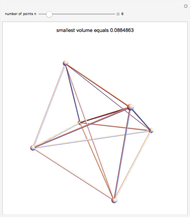
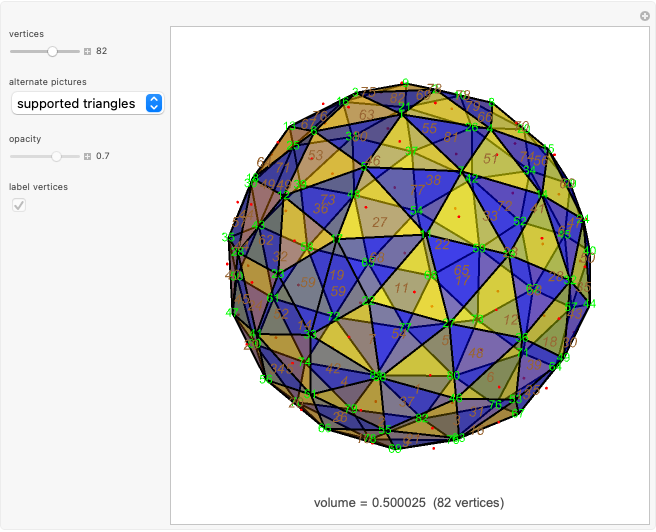
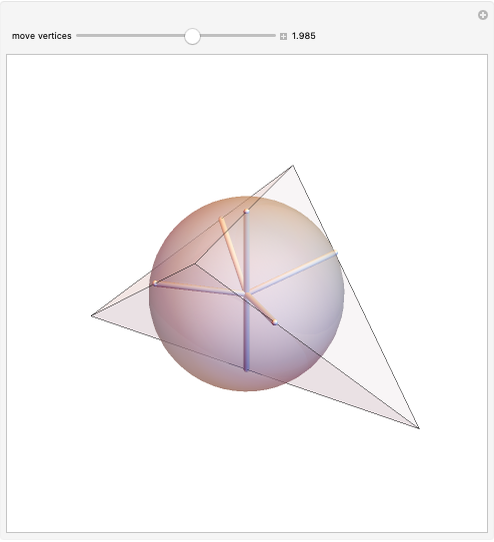
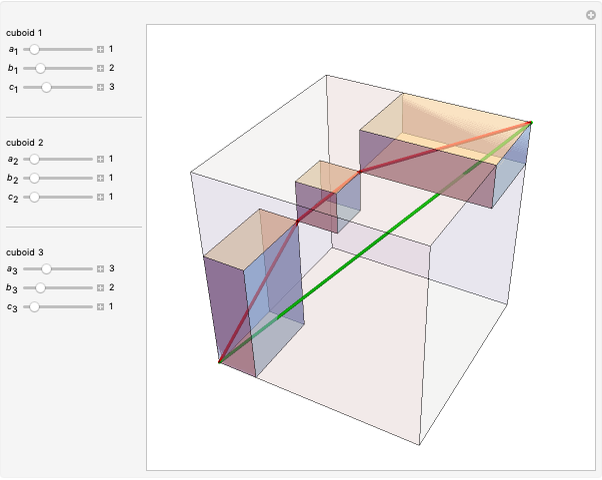
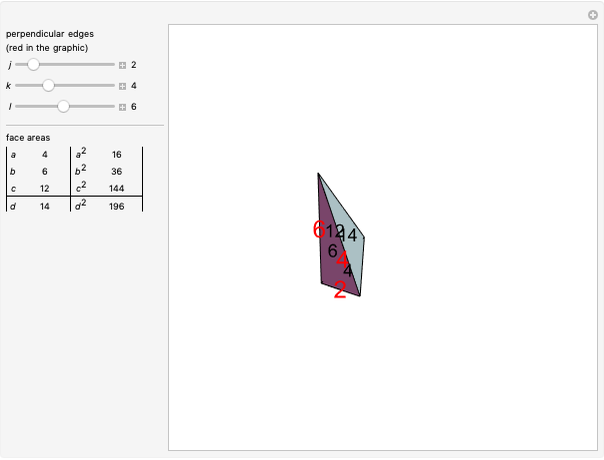
A polyhedron has 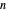 vertices. The greatest distance between vertices is 1. What is the maximum volume of the polyhedron? This is known as the biggest little polyhedron problem.
vertices. The greatest distance between vertices is 1. What is the maximum volume of the polyhedron? This is known as the biggest little polyhedron problem.
Contributed by: Ed Pegg Jr (November 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
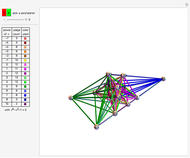
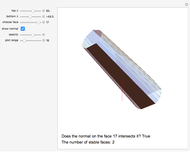
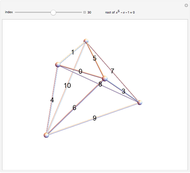
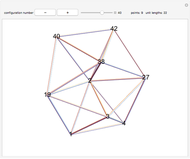
The unit-rod polyhedron shows a rod between all vertex pairs a unit distance apart.
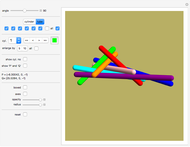
The unit-star picture builds polygons from half-unit rods meeting at a vertex.
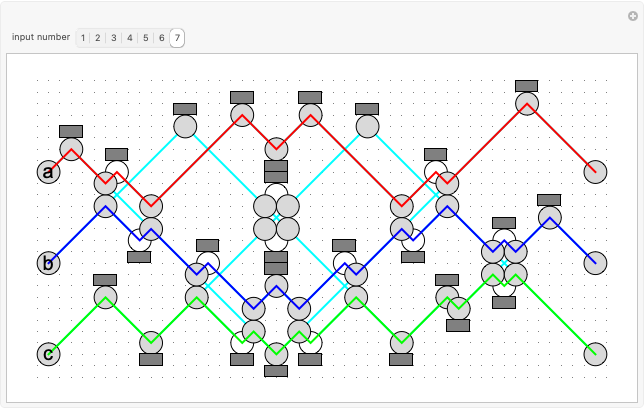
The unit-length graph shows how vertices a unit distance apart are connected.
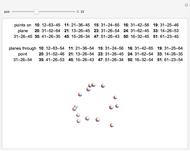
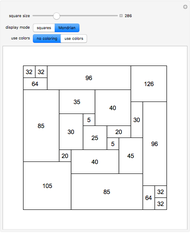
The planar vertex map puts the vertices on a sphere, then unrolls the sphere into a planar form.
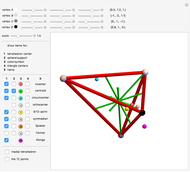
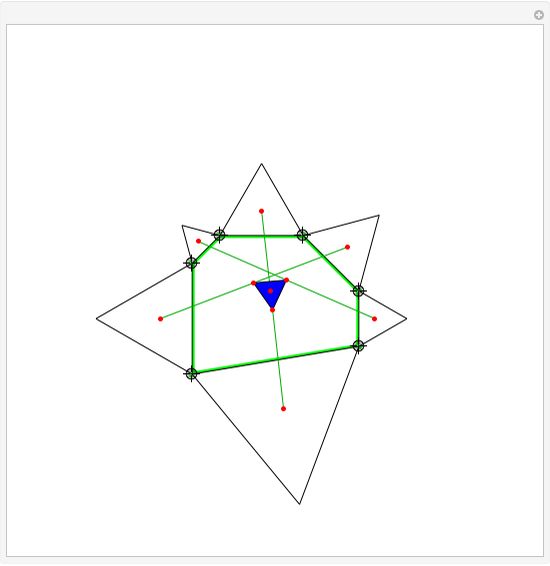
In the supported triangles image, all vertices of a blue triangle (with brown number) are at distance 1 from an opposing vertex with a matching green number.
The Initialization section contains various programs that may be able to improve some of the solutions.
References
[1] B. Kind and P. Kleinschmidt, "On the Maximal Volume of Convex Bodies with Few Vertices," Journal of Combinatorial Theory, Series A, 21(1) 1976 pp. 124–128. doi:10.1016/0097-3165(76)90056-X.
[2] A. Klein and M. Wessler, "The Largest Small 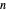 -dimensional Polytope with
-dimensional Polytope with 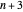 Vertices," Journal of Combinatorial Theory, Series A, 102(2), 2003 pp. 401–409. doi:10.1016/S0097-3165(03)00054-2.
Vertices," Journal of Combinatorial Theory, Series A, 102(2), 2003 pp. 401–409. doi:10.1016/S0097-3165(03)00054-2.
[3] A. Klein and M. Wessler, "A Correction to 'The Largest Small 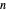 -dimensional Polytope with
-dimensional Polytope with 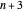 Vertices,'" Journal of Combinatorial Theory, Series A, 112(1), 2005 pp. 173–174. doi:10.1016/j.jcta.2005.06.001.
Vertices,'" Journal of Combinatorial Theory, Series A, 112(1), 2005 pp. 173–174. doi:10.1016/j.jcta.2005.06.001.
[4] E. Pegg Jr. "Biggest Little Polyhedra" from Wolfram Community—A Wolfram Web Resource. (Oct 28, 2015) community.wolfram.com/groups/-/m/t/463699.
[5] E. Pegg Jr. "Biggest Little Polyhedron—New Solutions in Combinatorial Geometry" from Wolfram Blog—A Wolfram Web Resource. (May 20, 2015) blog.wolfram.com/2015/05/20/biggest-little-polyhedronnew-solutions-in-combinatorial-geometry.
Permanent Citation