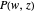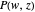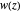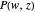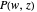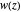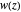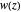Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

The Monodromy Group of an Algebraic Function

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

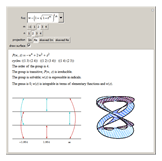
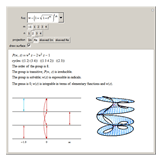
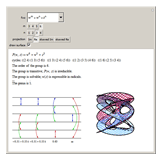
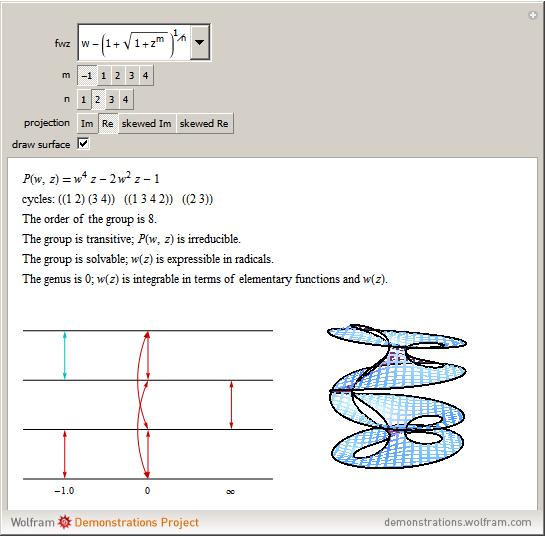
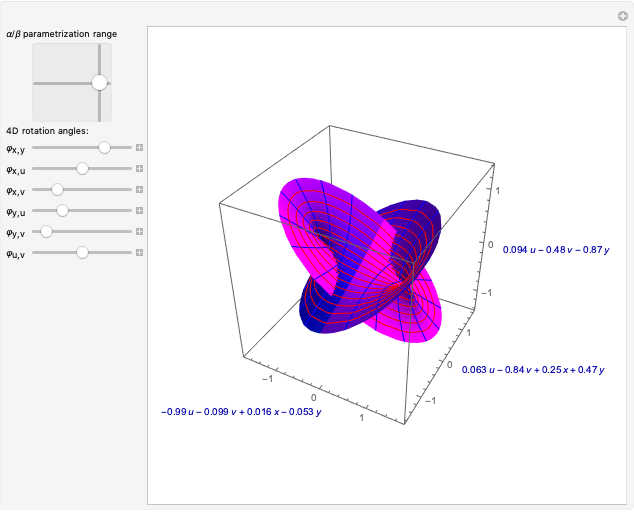
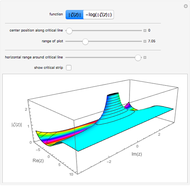
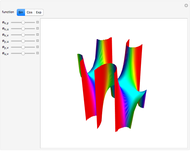
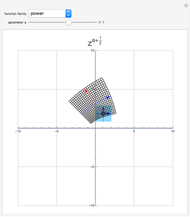
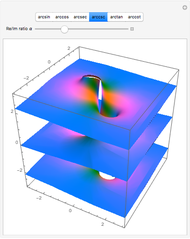
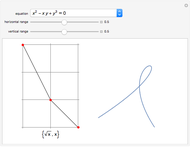
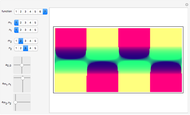
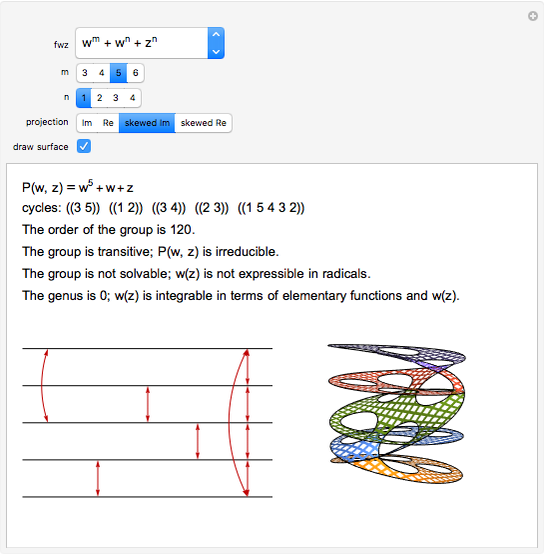
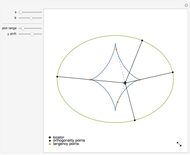
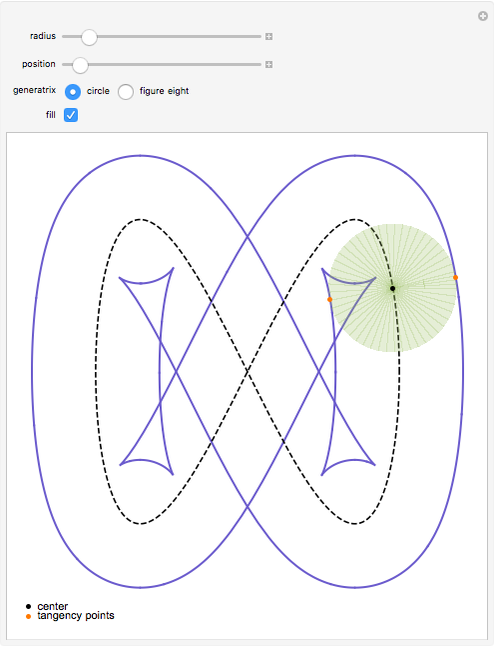
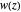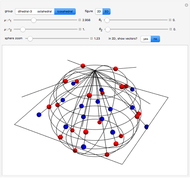
This Demonstration shows the structure of the branches of a multivalued function defined by a polynomial equation 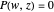, illustrating the transitions between the branches along paths going around a branch point. The actual configuration may depend on the choice of the branch cuts, but the group generated by the branch cycles is always the same. In general this group is a normal subgroup of the Galois group of 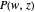over 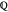. A number of important properties of 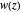can be inferred from the structure of the monodromy group:

[more]

• is absolutely irreducible if and only if the group is transitive;

• if is irreducible, can be expessed in radicals as a function of if and only if the group is solvable;

• the genus of can be computed from the branch cycles using the Riemann–Hurwitz formula. If is irreducible and the genus is zero, the integral of can always be expressed in terms of and elementary functions. (The converse is not true: it is possible for to have an elementary antiderivative if the genus is greater than zero.)

[less]

Contributed by: Maxim Rytin (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send