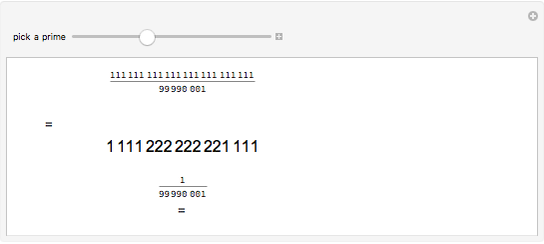
The Pigeonhole Principle - Repunits

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
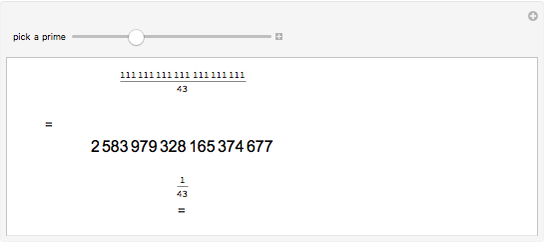
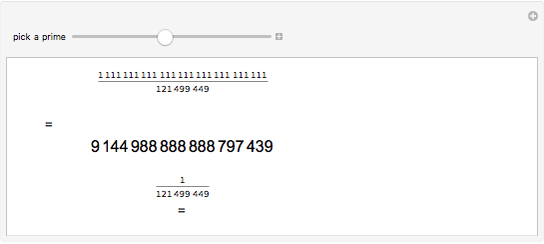
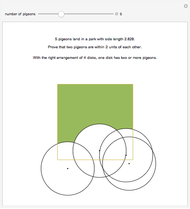
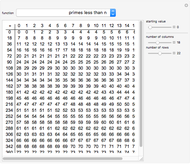
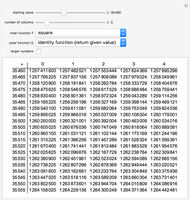
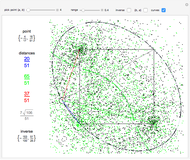
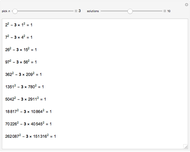
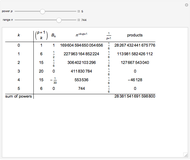
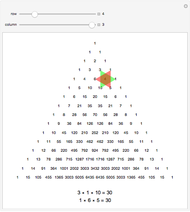
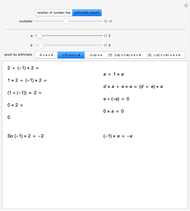
In 1834, Johann Dirichlet noted that if there are five objects in four drawers then there is a drawer with two or more objects. The Schubfachprinzip, or drawer principle, got renamed as the pigeonhole principle, and became a powerful tool in mathematical proofs.
[more]
Contributed by: Ed Pegg Jr (March 2011)
Open content licensed under CC BY-NC-SA
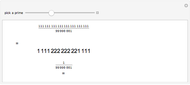
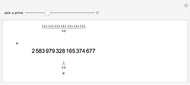
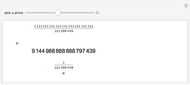
Snapshots
Details
detailSectionParagraphPermanent Citation
"The Pigeonhole Principle - Repunits"
http://demonstrations.wolfram.com/ThePigeonholePrincipleRepunits/
Wolfram Demonstrations Project
Published: March 7 2011