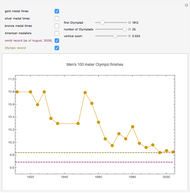
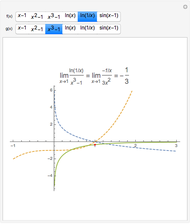
The Trinomial Distribution

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
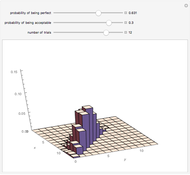
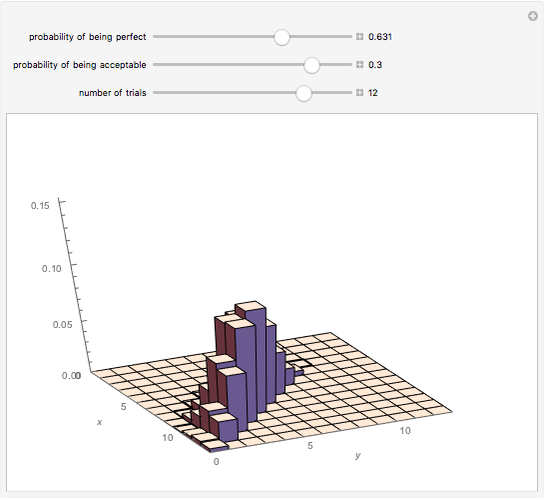
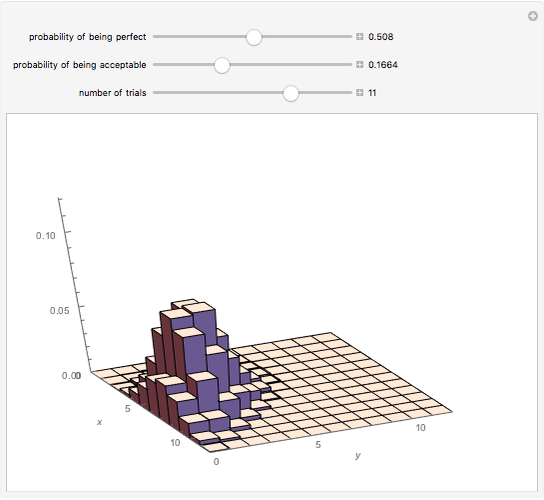
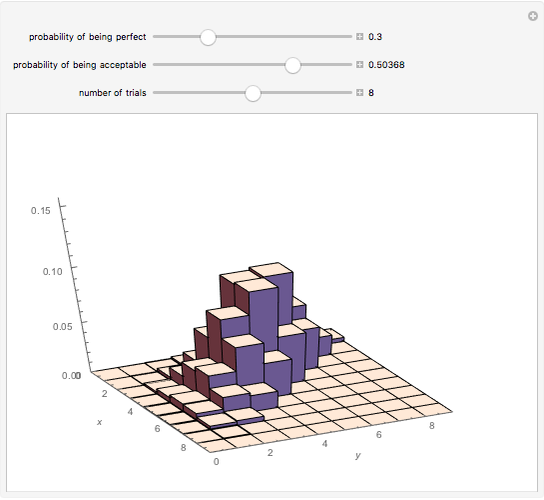
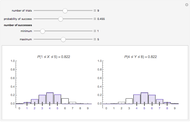
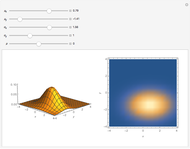
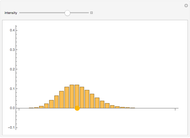
A binomial random variable models the number of successes in  trials, where the trials are independent and the only options on each trial are success and failure. A generalization of this called a multinomial distribution can be obtained by allowing more than two possibilities on each trial. When there are three possibilities on each trial, call them "perfect", "acceptable", and "failing", the result is a trinomial random variable. Letting
trials, where the trials are independent and the only options on each trial are success and failure. A generalization of this called a multinomial distribution can be obtained by allowing more than two possibilities on each trial. When there are three possibilities on each trial, call them "perfect", "acceptable", and "failing", the result is a trinomial random variable. Letting 
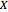 be the number of perfects and
be the number of perfects and 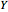 the number of acceptables in
the number of acceptables in  trials, the image is a rendering of the joint probability mass function of
trials, the image is a rendering of the joint probability mass function of 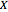 and
and 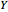 . The cuboid whose lower-left corner is at
. The cuboid whose lower-left corner is at 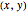 has height equal to the probability of
has height equal to the probability of  perfects and
perfects and 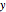 acceptables in
acceptables in  trials. Note that if
trials. Note that if 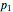 is the probability of a trial being perfect and
is the probability of a trial being perfect and 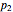 the probability of a trial being acceptable, then the probability of failure on the trial is
the probability of a trial being acceptable, then the probability of failure on the trial is 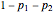 .
.
Contributed by: Chris Boucher (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"The Trinomial Distribution"
http://demonstrations.wolfram.com/TheTrinomialDistribution/
Wolfram Demonstrations Project
Published: March 7 2011