Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Three-Distance Theorem

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

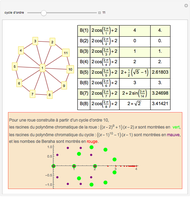
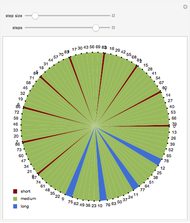
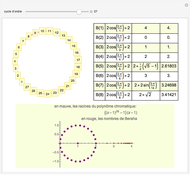
Let be a real number, and consider the arithmetic progression modulo 1. You can think of this as walking along a circle with steps of a fixed length. The three-distance theorem states that the distance between any two consecutive footprints is one of at most three distinct numbers. That is, the circle is partitioned into arcs with at most three distinct lengths.

Contributed by: Eric Rowland (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

If is rational, then eventually (namely when is the denominator of ), so the steps are then retraced. In this case there is eventually only one length between distinct consecutive points.

The interesting case is when is irrational. This is the so-called "irrational rotation", and there are either two or three distinct lengths.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send