Transformations of Relativistic Temperature: Planck-Einstein, Ott, Landsberg, and Doppler Formulas

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
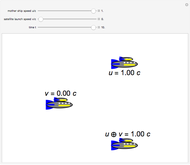
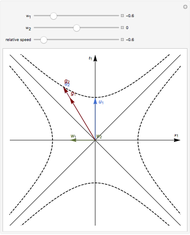
This Demonstration illustrates spacetime velocity vectors representing internal energy currents and their equilibration for a system of two relativistic thermodynamic bodies in 1+1 dimensions. The velocities of the two bodies are 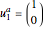 and
and 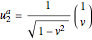 in units with
in units with  . The corresponding spacelike internal energy current vectors are
. The corresponding spacelike internal energy current vectors are  and
and 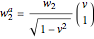 . The equilibration vectors are the sums
. The equilibration vectors are the sums  for
for 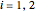 . In thermal equilibrium their directions become parallel.
. In thermal equilibrium their directions become parallel.
Contributed by: P. Ván and T. S. Bíró (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This Demonstration proposes a clarification of contradictory theoretical approaches to relativistic thermodynamics. According to our suggestion, a new concept of internal energy leads to thermodynamic equilibrium conditions that incorporate the existing propositions. You can manipulate spacetime vectors related to the intensive parameter 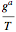 representing energy-momentum equilibration.
representing energy-momentum equilibration.
In equilibrium, two moving and interacting thermodynamic bodies obey 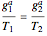 . In the coordinate system of the first body this condition can be expressed by the spacetime velocity vectors of body centers and energy currents as
. In the coordinate system of the first body this condition can be expressed by the spacetime velocity vectors of body centers and energy currents as 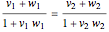 and
and 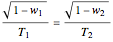 , respectively. The snapshots show famous particular cases for the relative speed
, respectively. The snapshots show famous particular cases for the relative speed  .
.
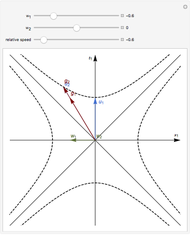
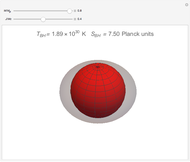
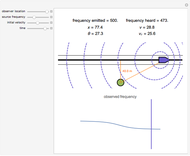
Snapshot 1: the Planck–Einstein equilibrium, when the energy current is carried by the moving body,  ; in this case the moving body appears cooler
; in this case the moving body appears cooler
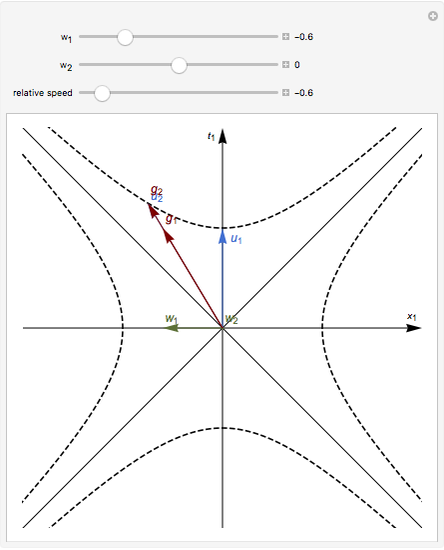
Snapshot 2: the Blanusa-Ott equilibrium, when the energy current stays with the observing body,  ; in this case the moving body appears hotter
; in this case the moving body appears hotter
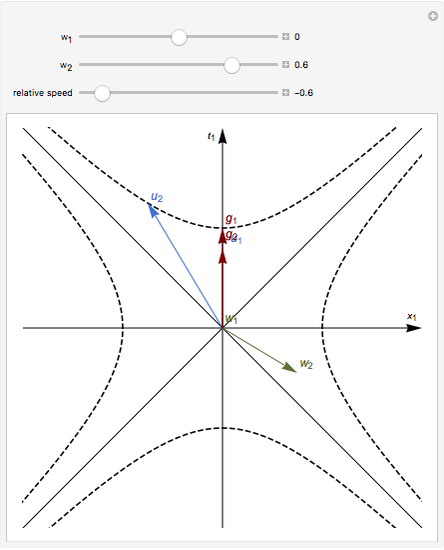
Snapshot 3: the Landsberg equilibrium, when the energy current velocities compensate each other inside the two bodies, 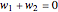 ; in this case the temperatures of the two moving bodies are equal
; in this case the temperatures of the two moving bodies are equal
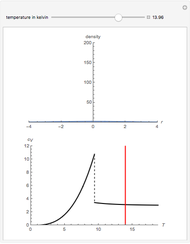
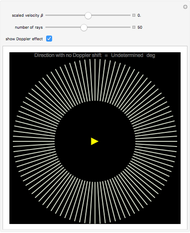
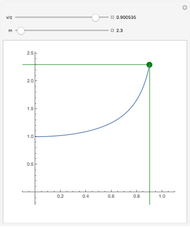
Snapshots 4 and 5: the Doppler blue shift and red shift ( ) equilibria, when the energy transfer is due to radiation,
) equilibria, when the energy transfer is due to radiation,  ,
, 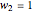 ; in these cases the temperatures of the two moving bodies are related by a Doppler shift
; in these cases the temperatures of the two moving bodies are related by a Doppler shift
For more information see T. S. Biró, P. Ván, "About the Temperature of Moving Bodies".
Permanent Citation