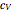Bose-Einstein Condensation in a Harmonic Trap
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
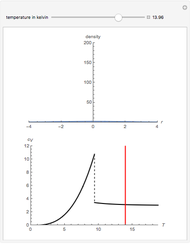
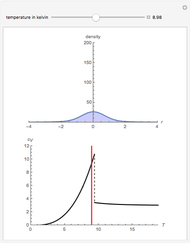
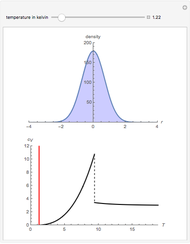
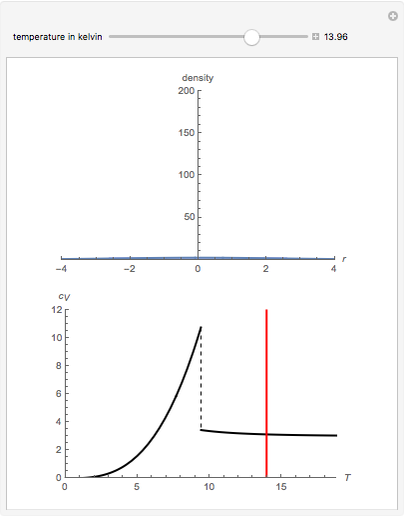
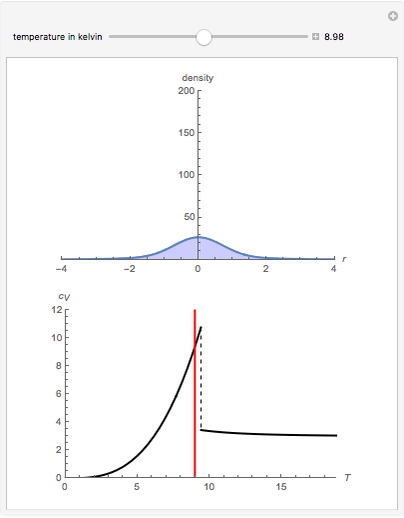
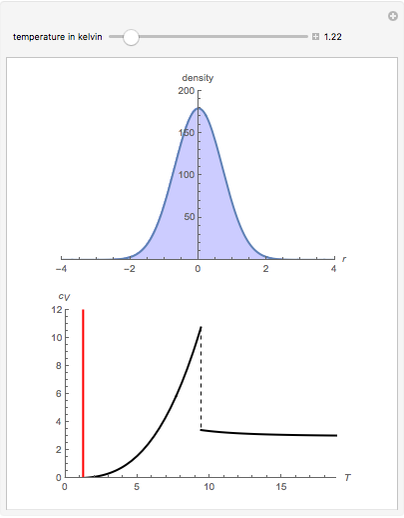
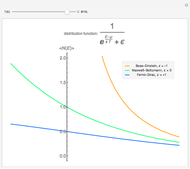
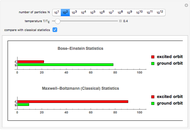
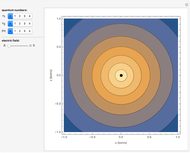
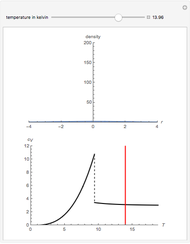
At ultra-cold temperatures, a gas of bosons undergoes a phase transition where there is a macroscopic occupation of the ground state. The top plot shows how the density profile of bosons in a 3D harmonic trap changes with temperature, 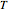 .
.
Contributed by: S. Andrew Gifford (October 2008)
Open content licensed under CC BY-NC-SA
Snapshots
Details
For more information, see the BEC homepage.
Permanent Citation