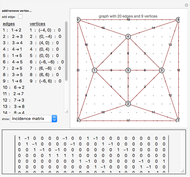
Trigrams and Real Clifford Algebras

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
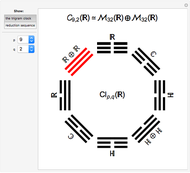
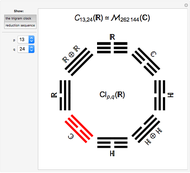
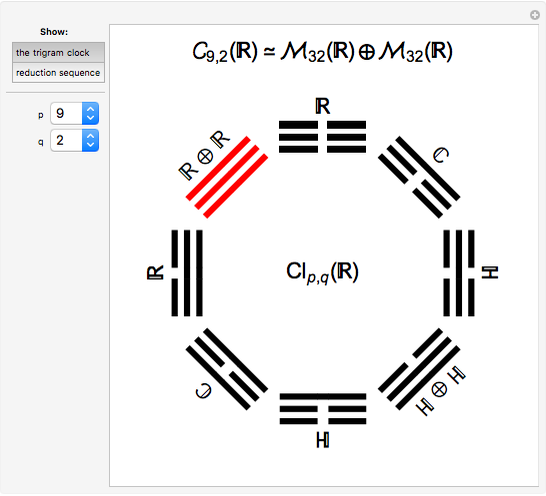
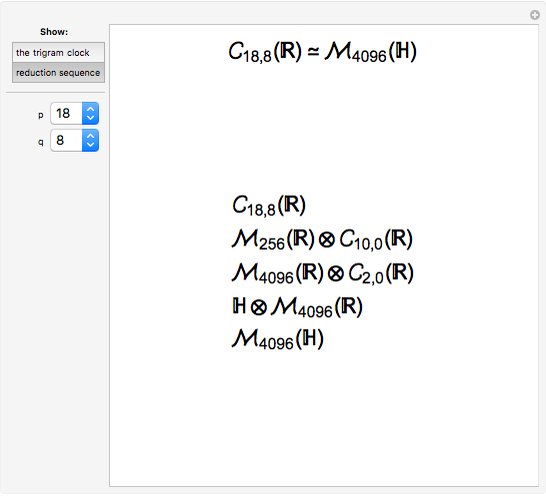
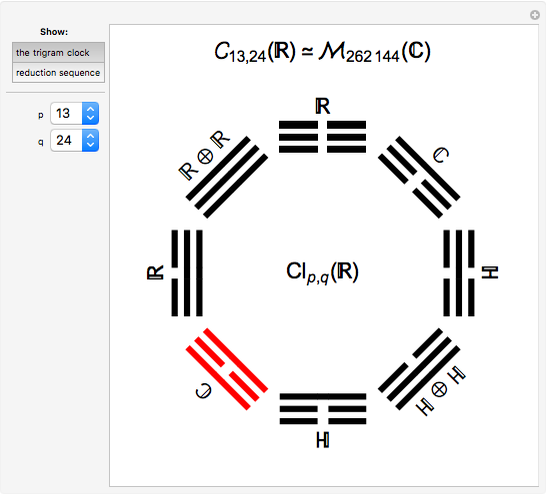
This Demonstration displays the classification of real Clifford algebras, making the eightfold periodicity manifest by mapping it onto a clock created from the eight trigrams used in the I Ching.
[more]
Contributed by: Simon Tyler (September 2010)
Open content licensed under CC BY-NC-SA
Snapshots
Details
We denote the real Clifford algebra of signature  as
as 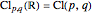 . It is most simply described as the free algebra over the reals constructed from the
. It is most simply described as the free algebra over the reals constructed from the  basis elements
basis elements 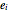 subject to the relations
subject to the relations
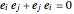 for
for  ,
,
 for
for  ,
,
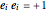 for
for 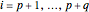 .
.
Note that this sign convention is the same as that used in MathWorld (Wolfram MathWorld), but opposite that used in Wikipedia.
It is easy to see that as a vector space, the algebra has the basis
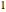 ,
, 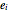 ,
,  (
(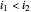 ), …,
), …, 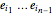 (
(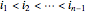 ),
), 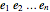
and is thus of real dimension  .
.
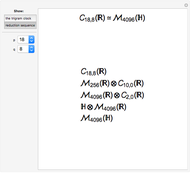
The classification of Clifford algebras is the process of realizing the above relations using matrices and matrix multiplication. The classification is tractable due to certain recurrence relations between the Clifford algebras, namely
(1): 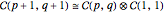 ,
,
(2): 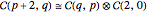 ,
,
(3): 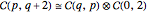 .
.
Isomorphism (1) allows an arbitrary Clifford algebra to be reduced to a product of  lots of
lots of 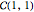 and either
and either 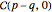 or
or 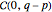 . Then isomorphisms
. Then isomorphisms 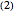 and
and  can reduce the latter factor to a product of powers of
can reduce the latter factor to a product of powers of  and powers of
and powers of 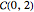 , and a remainder of
, and a remainder of 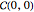 ,
,  , or
, or  . So we need the matrix realization of the remaining six, low-dimensional Clifford algebras.
. So we need the matrix realization of the remaining six, low-dimensional Clifford algebras.
Define the 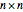 matrix algebra
matrix algebra 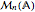 where
where 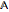 is either the reals (
is either the reals (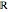 ), complexes (
), complexes ( ), or quaternions (
), or quaternions (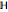 ) and note that
) and note that 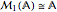 . Remember that both the complex and quaternionic numbers can themselves be realized as real matrix algebras of dimension 2 and 4 respectively.
. Remember that both the complex and quaternionic numbers can themselves be realized as real matrix algebras of dimension 2 and 4 respectively.
Direct calculation gives the results
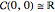 ,
, 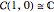 ,
, 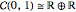 ,
, 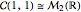 ,
,  ,
, 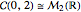 .
.
To simplify and complete the matrix realization we use the following isomorphisms between the various products of matrix algebras
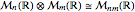 ,
, 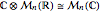 ,
, 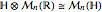 ,
, 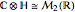 ,
, 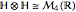 .
.
The eightfold periodicity displayed in the clock is a consequence of (2) and (3), from which we can derive the relations
 and
and 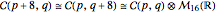 .
.
This eightfold periodicity was discovered by Cartan in 1908, but is often given the name Bott periodicity due to related periodicities found by Bott in the late 1950s in the study of the homotopy groups of the classical groups.
The trigrams in the Yì Jīng (I Ching) can be associated with the obvious binary sequence where - - (associated with yin) is given the value  and — (associated with yang) is valued at
and — (associated with yang) is valued at 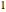 . Then a binary digit is constructed with the smallest position at the top. Our clock follows that binary sequence and for the Clifford Algebra
. Then a binary digit is constructed with the smallest position at the top. Our clock follows that binary sequence and for the Clifford Algebra 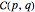 it points to the position
it points to the position  . The actual order normally given to trigrams does not match the binary correspondence given above.
. The actual order normally given to trigrams does not match the binary correspondence given above.
In the Yi Jing each trigram is given a value in a range of areas (direction, family, body part, animal, etc.) and then combined into pairs call hexagrams. The meaning of a hexagram is inherited from its component trigrams. The lower trigram is called the inner and is linked to the personal aspects, while the upper trigram is called the outer and linked to the external aspects. Thus a large range of characteristics and situations can be encoded using these hexagrams.
This Demonstration was inspired by a graphic found on a page by Tony Smith (www.valdostamuseum.org).
References
[1] M. Rausch de Traubenberg. "Clifford Algebras in Physics." (2005) http://arxiv.org/abs/hep-th/0506011.
[2] J. Baez, "Octonions," Bulletin of the American Mathematical Society, 39, 2002 pp. 145–205.
[3] W. K. Clifford, "On the Classification of Geometric Algebras," Mathematical Papers of W. K. Clifford (R. Tucker, ed.), London: MacMillan, 1882.
[4] É. Cartan, "Nombres Complexes," Encyclopédie des Sciences Mathématiques, Vol. 1 (J. Molk, ed.), Paris: Gauthier–Villars, 1908 pp. 329–468.
Permanent Citation