Two Electrons in a Box: Wavefunctions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
The one-dimensional analog of the Coulomb potential, 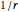 , is the absolute value function,
, is the absolute value function, 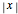 . Two electrons (at locations
. Two electrons (at locations  and
and 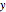 ) restricted to a one-dimensional
) restricted to a one-dimensional  -unit-width box repel each other with a potential proportional to
-unit-width box repel each other with a potential proportional to 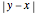 . The one-dimensional Schrödinger equation is mathematically identical to the corresponding two-dimensional Schrödinger equation for a single electron moving in a
. The one-dimensional Schrödinger equation is mathematically identical to the corresponding two-dimensional Schrödinger equation for a single electron moving in a  -unit-square box experiencing the potential
-unit-square box experiencing the potential  with
with 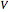 a strength parameter. The potential has
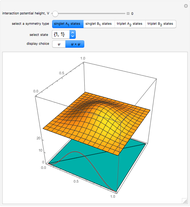
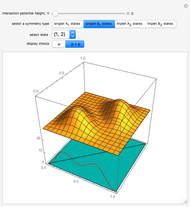
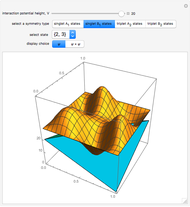
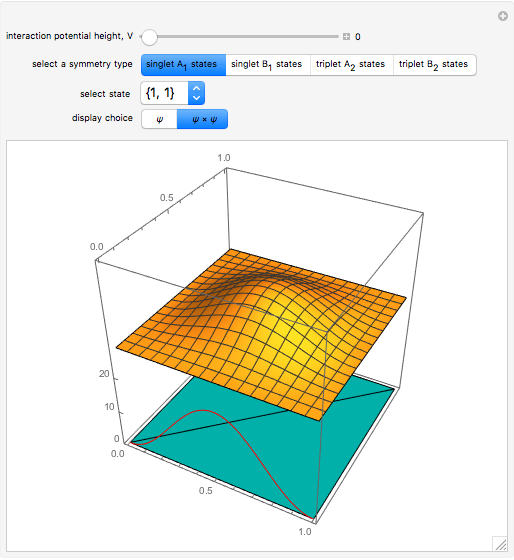
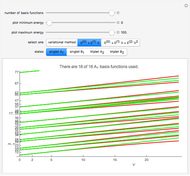
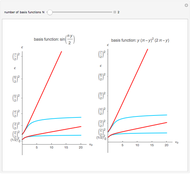
a strength parameter. The potential has 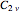 symmetry and the wavefunctions must share this symmetry. Approximate wavefunctions are found using the variational method with appropriate linear combinations of the 49 basis functions
symmetry and the wavefunctions must share this symmetry. Approximate wavefunctions are found using the variational method with appropriate linear combinations of the 49 basis functions 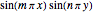 ,
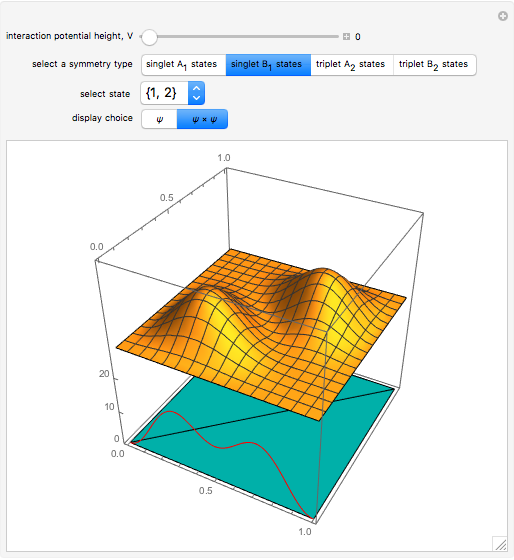
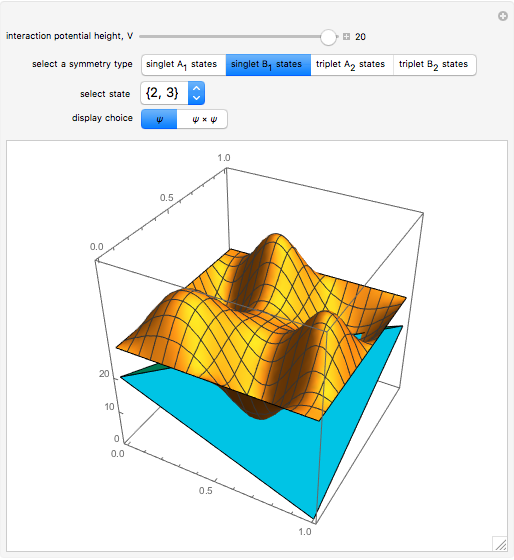
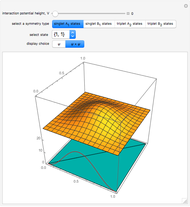
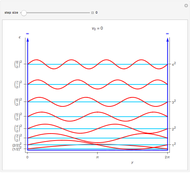
,  . The Demonstration shows the potential together with either the wavefunction
. The Demonstration shows the potential together with either the wavefunction 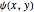 or its square
or its square 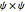 for various values of the potential parameter. If the display choice is for
for various values of the potential parameter. If the display choice is for 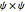 , the one-dimensional density function
, the one-dimensional density function 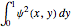 is shown in red on the
is shown in red on the  surface of the displayed cube.
surface of the displayed cube.
Contributed by: M. Hanson (July 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The potential function 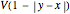 has a twofold rotation axis located at
has a twofold rotation axis located at 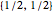 . Functions that are symmetric with respect to this operation are designated as having
. Functions that are symmetric with respect to this operation are designated as having 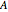 symmetry; if antisymmetric,
symmetry; if antisymmetric, 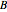 symmetry. The potential has a mirror plane,
symmetry. The potential has a mirror plane, 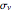 , containing the
, containing the  axis and the line
axis and the line  . The paired electron or singlet states must be symmetric with respect to
. The paired electron or singlet states must be symmetric with respect to 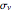 . The unpaired electron or triplet states are antisymmetric with respect to
. The unpaired electron or triplet states are antisymmetric with respect to 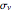 . The
. The 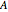 and
and 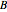 states are each subdivided into
states are each subdivided into 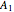 ,
,  ,
,  , and
, and 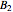 states. The states with subscript 1 are symmetric with respect to
states. The states with subscript 1 are symmetric with respect to 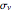 . The states with subscript 2 are antisymmetric with respect to
. The states with subscript 2 are antisymmetric with respect to 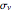 . There is another mirror plane,
. There is another mirror plane,  , containing the line
, containing the line 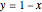 and the
and the  axis.
axis.
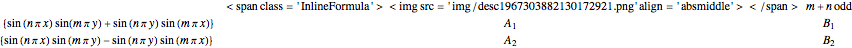
Permanent Citation