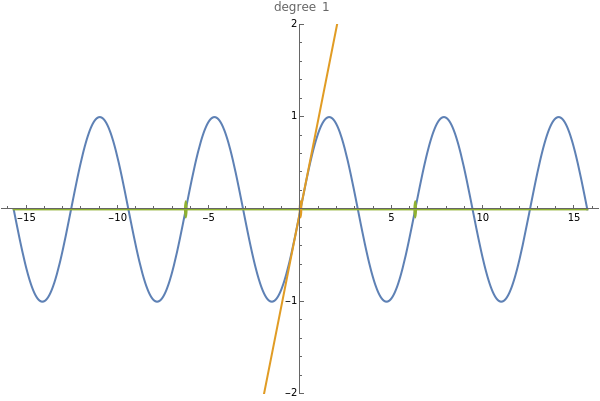
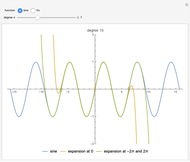
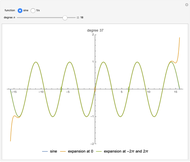
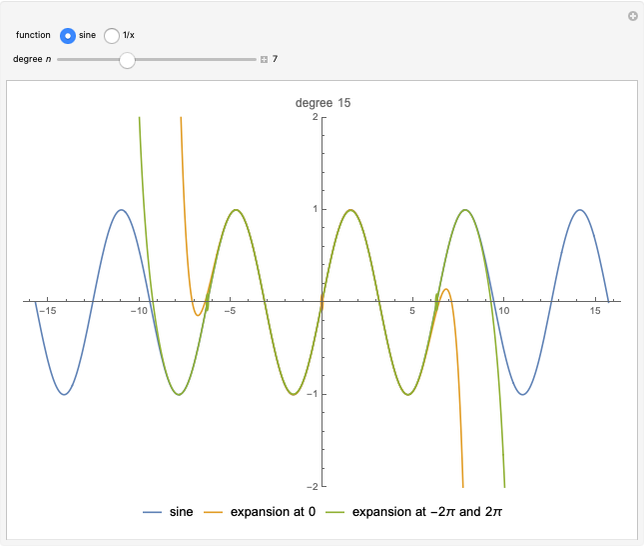
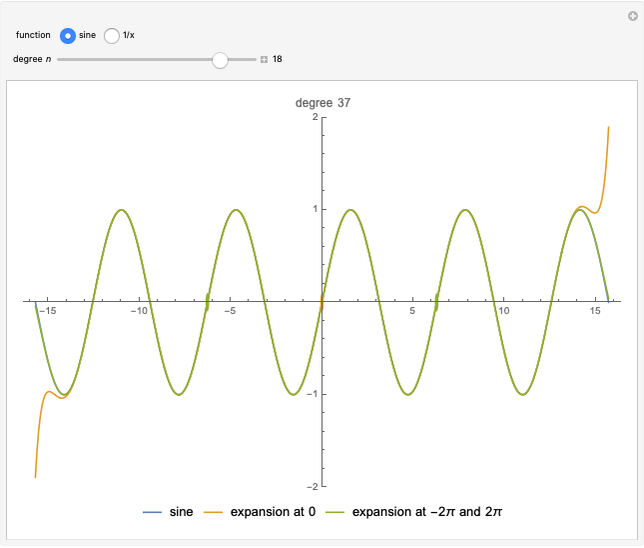
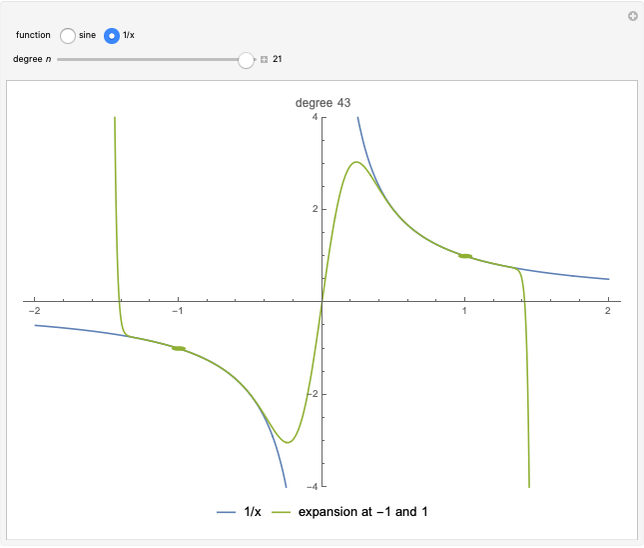
This Demonstration calculates recursively the two-point Taylor expansion (2pTE) of a function, which is a polynomial expansion around two reference points. This expansion is increasingly accurate as the number of steps in the recursion progresses. 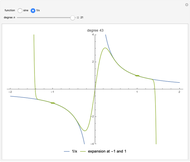This block shows two examples of the 2pTE applied to two different functions as the degree of the fitting polynomial increases: One is the expansion of the sine function at the points and , while the standard one-point Taylor expansion around is shown for comparison. The second example is the expansion of the reciprocal function at the points and .