Uniaxial-Biaxial Birefringence: Geometrical Constructions for Optical EM Waves

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Electromagnetic (EM) waves propagating through birefringent media experience two indices of refraction, 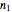 and
and 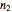 , that are functions of the propagation direction and polarization mode. This Demonstration presents two geometrical constructions (the index ellipsoid and the normal surface) that graphically solve for
, that are functions of the propagation direction and polarization mode. This Demonstration presents two geometrical constructions (the index ellipsoid and the normal surface) that graphically solve for 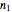 and
and 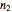 and exhibit selected EM vectors (electric displacement
and exhibit selected EM vectors (electric displacement 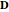 and Poynting vector
and Poynting vector  ), leading toward a full description of the EM wave. The results are presented in two coordinate systems: a global/lab frame (or LCS) for comparison when reorienting and a medium/principal frame (or PCS) that exploits the geometry.
), leading toward a full description of the EM wave. The results are presented in two coordinate systems: a global/lab frame (or LCS) for comparison when reorienting and a medium/principal frame (or PCS) that exploits the geometry.
Contributed by: Sotiris Danakas (January 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The propagation of an EM wave through matter is governed by Maxwell's four equations
 ,
,
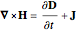 ,
,
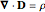 ,
,
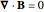 ,
,
and the three constitutive/material equations (low intensities/linear regime, no magnetoelectric effect)
 ,
,
 ,
,
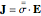 ,
,
where  is the relative electric permittivity tensor,
is the relative electric permittivity tensor,  is the electric conductivity tensor, and
is the electric conductivity tensor, and  is the relative magnetic permeability tensor.
is the relative magnetic permeability tensor.
For analytic solutions we need to make assumptions both for the transmitted EM waves and the properties of the media. At optical frequencies with monochromatic (or narrow spectral bandwidth) collimated beams of low intensity, usually we encounter transparent media with the following properties: linear (induced polarization is analogous to  ), nonabsorbing (
), nonabsorbing ( is real and symmetric), nondispersive, nonconducting (dielectric), magnetically isotropic (
is real and symmetric), nondispersive, nonconducting (dielectric), magnetically isotropic ( is a scalar and
is a scalar and 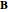 is parallel to
is parallel to 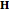 ), homogeneous, and away from EM sources (charges and currents).
), homogeneous, and away from EM sources (charges and currents).
Furthermore, many optical media (e.g. lenses) are isotropic and the tensor  reduces to a scalar. This considerably simplifies the math:
reduces to a scalar. This considerably simplifies the math: 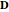 is parallel to
is parallel to  and the medium has only one index of refraction independent of the propagation direction and polarization mode.
and the medium has only one index of refraction independent of the propagation direction and polarization mode.
There is, however, a group of dielectrics of technological significance (crystals of certain symmetry, crystalline liquids, polymers) that are magnetically isotropic ( is a scalar) but electrically anisotropic (
is a scalar) but electrically anisotropic ( is a tensor). In this media group,
is a tensor). In this media group, 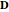 and
and  not parallel in the propagating EM wave (but
not parallel in the propagating EM wave (but 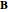 remains parallel to
remains parallel to 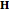 ), with the exception of certain directions defining the optic axes.
), with the exception of certain directions defining the optic axes.
Ordered media like crystals have three principal refractive indices (specific to the crystal structure) in the directions of the principal axes. Together these constitute the principal coordinate system (PCS), in which the permittivity tensor is diagonal. If all three indices are the same, the medium is characterized as isotropic; if two are the same, as uniaxial; and if all three are different, as biaxial. Uniaxial and biaxial media, which are the focus here, present the interesting and counterintuitive property of two indices of refraction that also depend on the EM wave's direction of propagation and polarization state. This physical property is known as birefringence. Further consequences of birefringence include double refraction, spatial walk-off, and modified Snell's law. Optical waveplates, beam splitters, and group velocity delay compensation plates are only a few of the optical devices whose operation is based on birefringence.
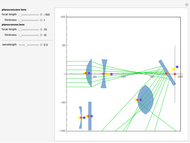
This Demonstration illustrates the two geometrical constructions that can be used to provide a visual solution to the mathematical problem of finding the two indices of refraction and the polarization vector for an EM wave propagating inside an electrically anisotropic media as a function of the propagation direction. Two coordinate systems can be used. First, the rotatable PCS frame (attached to the medium) that exploits symmetry and simplifies the math (e.g. 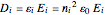 with
with 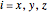 ). Second, a fixed reference frame (lab frame or LCS) that serves as a global reference frame and permits direct comparison of vector quantities even after reorientation. You can freely rotate the PCS frame in space to any orientation (compared to LCS) using three rotation angles. Multiple rotations are applied sequentially: first around the medium's
). Second, a fixed reference frame (lab frame or LCS) that serves as a global reference frame and permits direct comparison of vector quantities even after reorientation. You can freely rotate the PCS frame in space to any orientation (compared to LCS) using three rotation angles. Multiple rotations are applied sequentially: first around the medium's  axis, then around the new
axis, then around the new 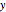 axis (
axis (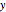 '), and finally around the final medium (
'), and finally around the final medium ( '')
'')  axis for an intrinsic rotation scheme
axis for an intrinsic rotation scheme  -
-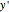 -
-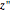 .
.
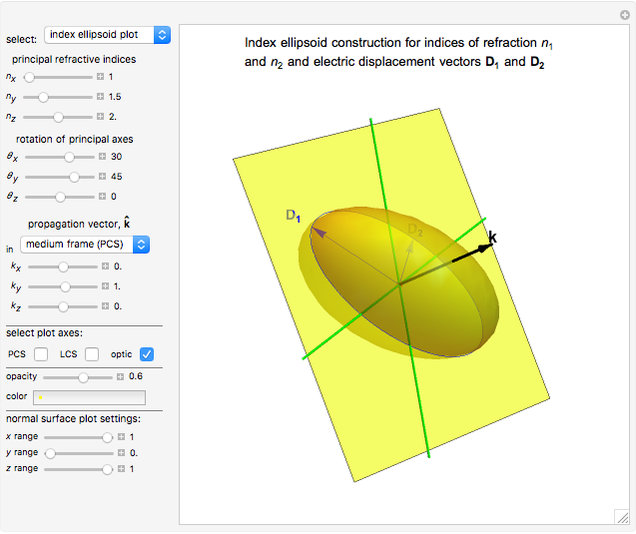
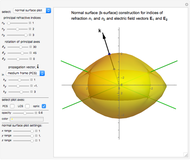
Index ellipsoid construction: The electric energy density 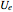 can be written (in PCS) as
can be written (in PCS) as
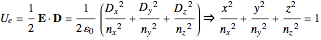 ,
,
where a transformation of axes has taken place with 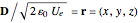 .
.
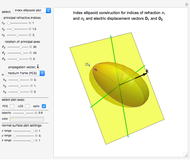
The constant electric energy surface is an ellipsoid in 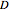 -space, known as the index ellipsoid or optical indicatrix, with the lengths of its semi-axes being the three indices of refraction of the anisotropic medium. In the case of a uniaxial medium, the surface simplifies to an ellipsoid of revolution, and in the isotropic case to a sphere.
-space, known as the index ellipsoid or optical indicatrix, with the lengths of its semi-axes being the three indices of refraction of the anisotropic medium. In the case of a uniaxial medium, the surface simplifies to an ellipsoid of revolution, and in the isotropic case to a sphere.
For each wave vector  , the plane normal to
, the plane normal to  intersects the ellipsoid in an ellipse, known as the index ellipse. It can be proven that the lengths of its two semi-axes are the two indices of refraction,
intersects the ellipsoid in an ellipse, known as the index ellipse. It can be proven that the lengths of its two semi-axes are the two indices of refraction, 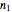 and
and 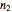 , corresponding to the particular
, corresponding to the particular  and the directions of the semi-axes are proportional to
and the directions of the semi-axes are proportional to 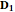 and
and 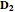 vectors of the EM wave (they are mutually perpendicular). It is a rather straightforward derivation then, from
vectors of the EM wave (they are mutually perpendicular). It is a rather straightforward derivation then, from  ,
, 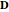 , and
, and  to recover
to recover 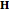 ,
,  ,
,  , where
, where  is the Poynting vector (
is the Poynting vector (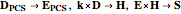 ).
).
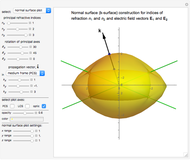
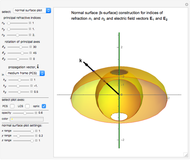
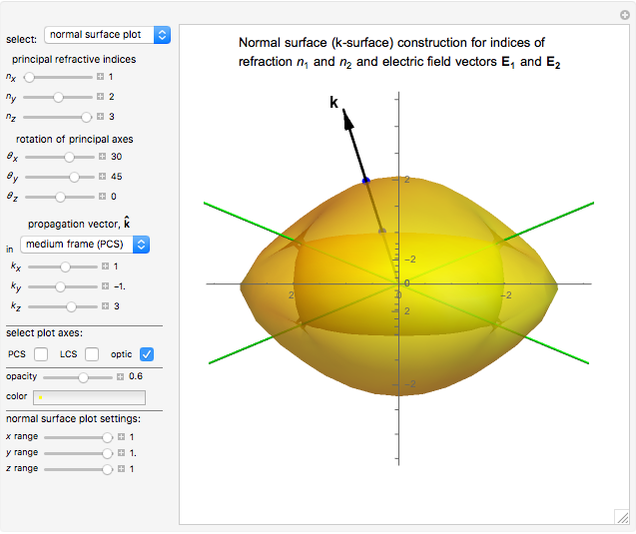
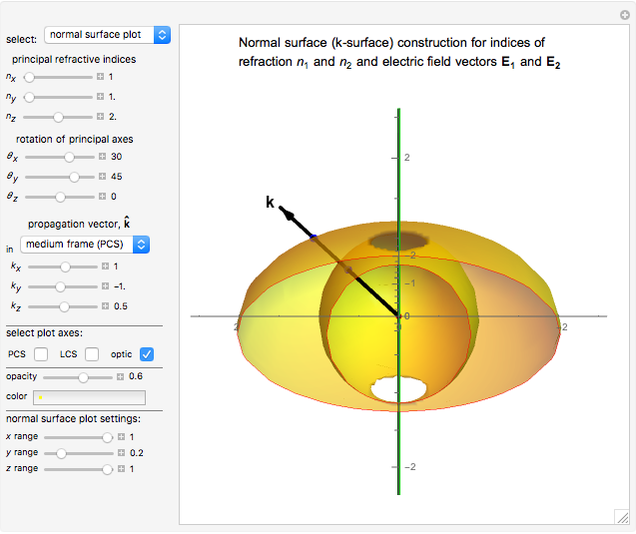
Normal surface construction: Combining the first two Maxwell's equations with the first constitutive relation results in
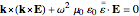 ,
,
In the medium coordinate frame (PCS), it is straightforward to convert the vector equation above to a homogeneous system of three linear equations in three unknowns, namely 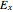 ,
,  , and
, and  . For the system to have nontrivial solutions the determinant of the coefficients must be zero. This results in an equation (in units of
. For the system to have nontrivial solutions the determinant of the coefficients must be zero. This results in an equation (in units of  ) that the components of the wave vector must satisfy for a specific
) that the components of the wave vector must satisfy for a specific  and is known as the dispersion relation, a biquadratic equation in
and is known as the dispersion relation, a biquadratic equation in  . This relation represents a surface of two sheets known as the normal surface or
. This relation represents a surface of two sheets known as the normal surface or  -surface. Each direction of propagation
-surface. Each direction of propagation 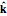 intersects the two sheets at two points, creating two collinear vectors (from the origin to the points of intersection) representing the allowed wave vectors and their lengths, the two indices of refraction. Furthermore, the gradient of the surface at each intersection point is proven to be the direction of the Poynting vector (indicated in the results section by
intersects the two sheets at two points, creating two collinear vectors (from the origin to the points of intersection) representing the allowed wave vectors and their lengths, the two indices of refraction. Furthermore, the gradient of the surface at each intersection point is proven to be the direction of the Poynting vector (indicated in the results section by  ). With
). With  at hand we can solve the system of equations and obtain the directions of
at hand we can solve the system of equations and obtain the directions of 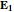 and
and 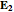 , and we can derive
, and we can derive 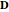 ,
, 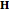 , and
, and  algebraically.
algebraically.
A few remarks on the accuracy of the results. Both produce practically identical results with high accuracy almost under any initial conditions.
Deviations between the two methods can be found only when the propagation vector is along an optic axis due to intrinsic limitations:
▪ in the normal surface construction, the Poynting vector  being the gradient of the surface at a singular point becomes inaccurate, but all other quantities remain highly reliable as they are obtained algebraically.
being the gradient of the surface at a singular point becomes inaccurate, but all other quantities remain highly reliable as they are obtained algebraically.
▪ In the index ellipsoid construction, the index ellipse collapses to a circle, thus losing the polarization information that the ellipse's axes provided. In this very rare occasion the normal surface method is still reliable, as pointed out above.
Snapshot 1: normal surface construction for a biaxial medium
Snapshot 2: normal surface construction for a uniaxial medium
Snapshot 3: index ellipsoid construction for a biaxial medium with the wave vector along one of the principal axes
References
[1] M. Born and E. Wolf, Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light, 7th ed., Cambridge: Cambridge University Press, 2003.
[2] A. Yariv and P. Yeh, Optical Waves in Crystals: Propagation and Control of Laser Radiation, Hoboken, NJ: John Wiley & Sons, 2003.
[3] J. F. Nye, Physical Properties of Crystals: Their Representation by Tensors and Matrices, Oxford: Oxford University Press, 2000.
[4] B. E. A. Saleh and M. C. Teich, Fundamentals of Photonics, 2nd ed., Hoboken, NJ: John Wiley & Sons, 2007.
Permanent Citation