Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Using Paperfolding to Transform Stars into Clouds

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

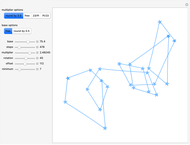
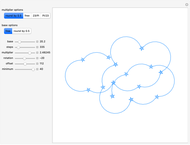
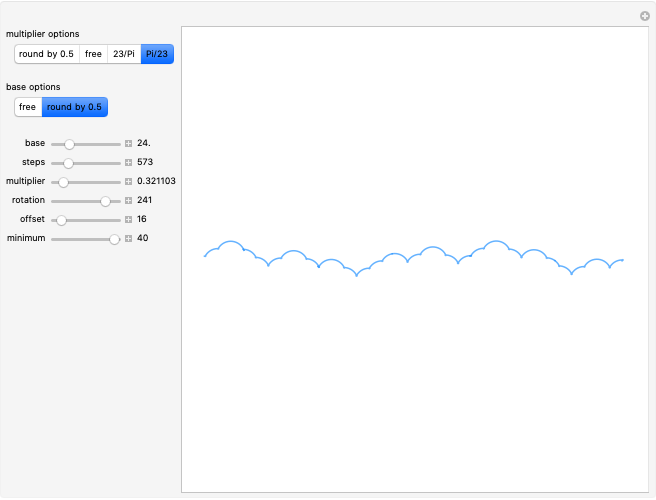
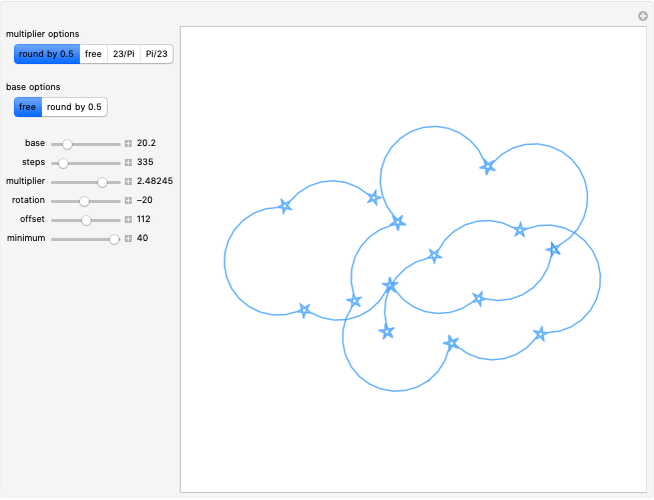
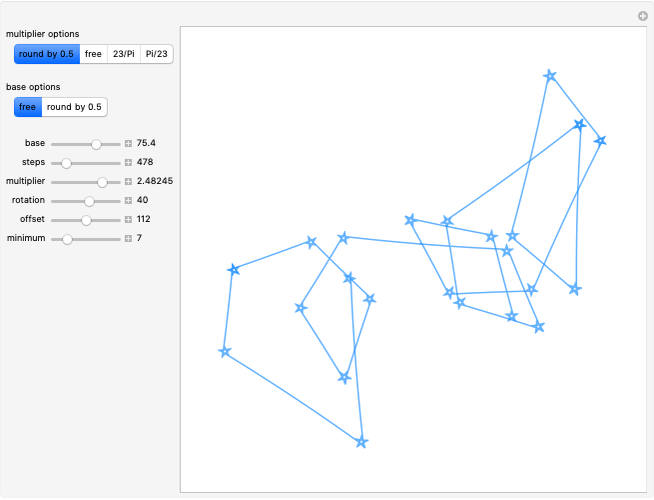
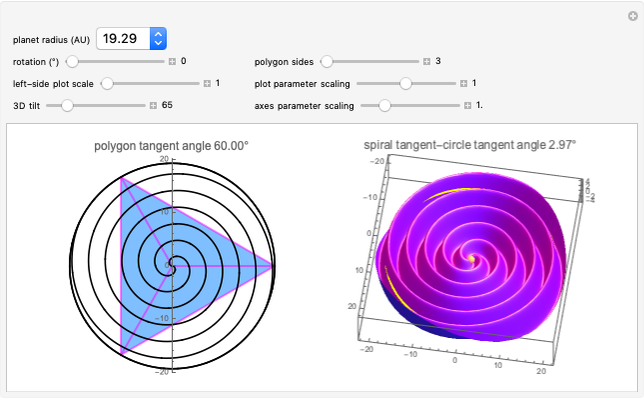
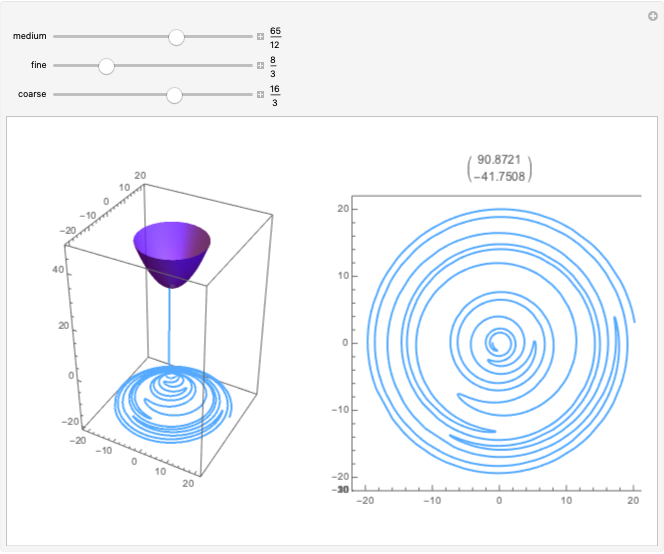
Math is art, and art is math. This Demonstration shows how changing parameter values for an angle path table containing the Rudin–Shapiro sequence can transform patterns resembling star constellations into clouds. Changing the path length is the digital equivalent of drawing or erasing lines on paper. The specific paths that can be created in this Demonstration also include dragon curves, as shown in [1]. The AnglePath function transforms the table of values into turtle graphics, which defines changes in the direction of a path with respect to the position rather than a fixed point in space. The turtle graphics concept has applications in robotics and machine learning. The blue color of the path is an homage to a string of blue star shapes from Egypt circa 1981–1295 B.C. [2].

Contributed by: Alexandra L. Brosius (May 2021)
Open content licensed under CC BY-NC-SA

Snapshots

Details

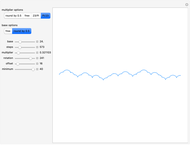
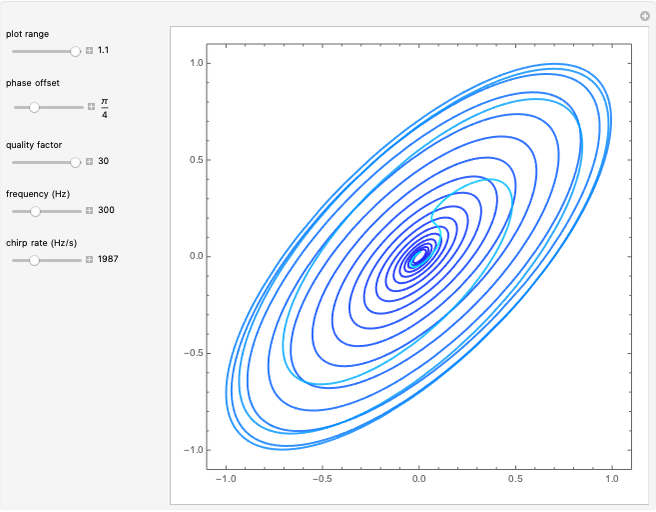
The seemingly random patterns in this Demonstration can resemble celestial constellations, clouds and abstract art. The point coordinates from the AnglePath function can act as a hodogram of a synthetic time series. The hodogram we use is a parametric plot of two perturbation components with respect to time, also useful for waveform analysis. Use the "offset" slider to switch between messy cloud-like waveforms and star-like waveforms with seemingly aperiodic spikes. When working with time series measurements, spikes are often indicative of artificial signals that need to be removed with a specialized filter. The parameter flexibility of RudinShapiro output may provide a new means of testing wave analysis software.

References

[1] "Paperfolding Dragon Curve" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/PaperfoldingDragonCurve.

[2] The Metropolitan Museum of Art. "String of Star Amulets, ca. 1981–1295 B.C." (Mar 3, 2021) www.metmuseum.org/art/collection/search/557492.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send