Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Voronoi Diagrams on Three-Dimensional Surfaces

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

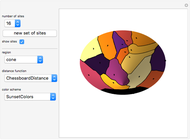
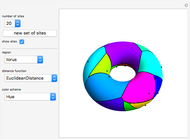
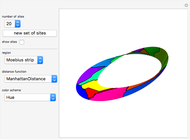
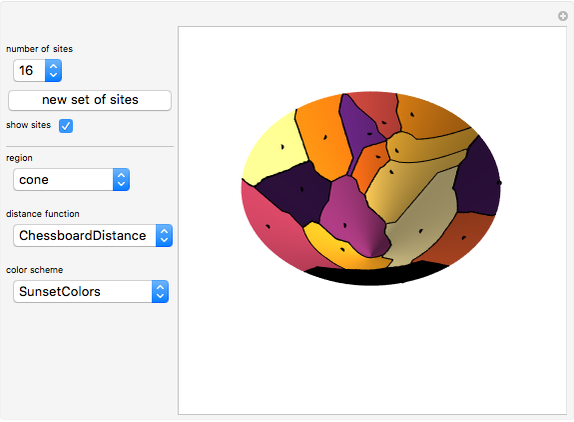
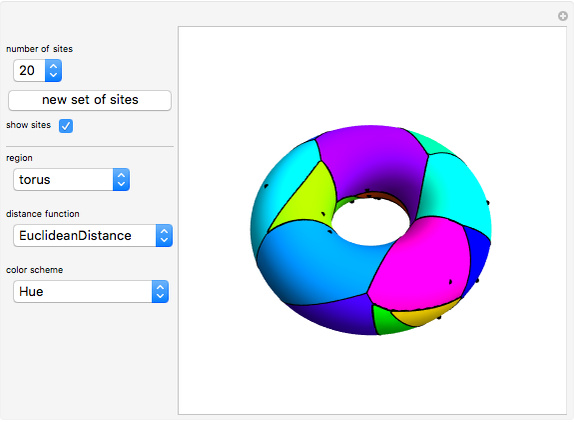
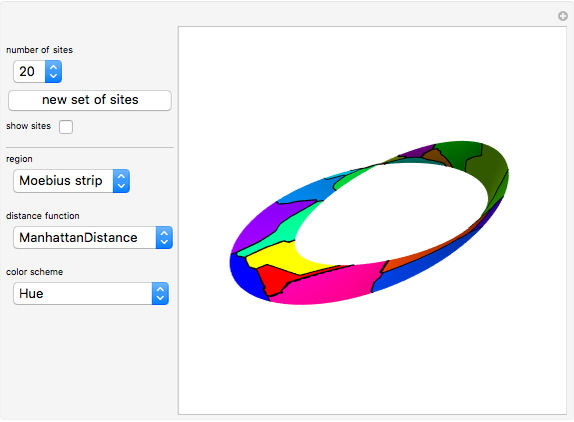
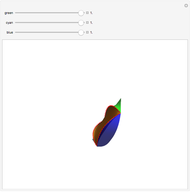
This Demonstration partitions the surface of a cylinder, cone, Möbius strip, sphere, or torus into Voronoi cells based on a set of up to 24 random points (sites) uniformly distributed over the surface.

[more]

You can choose from three different distance functions (Euclidean, Manhattan, or chessboard). You can choose the cell colors according to eight color schemes.

[less]

Contributed by: Erik Mahieu (July 2016)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The regions are created using Mathematica's built-in function ParametricPlot3D. NearestFunction using the selected DistanceFunction is used as a MeshFunction to partition the regions into Voronoi cells.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send