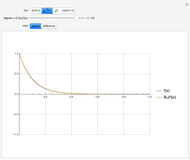
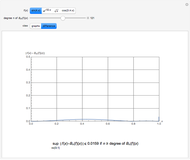
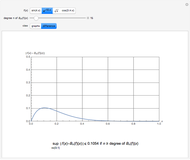
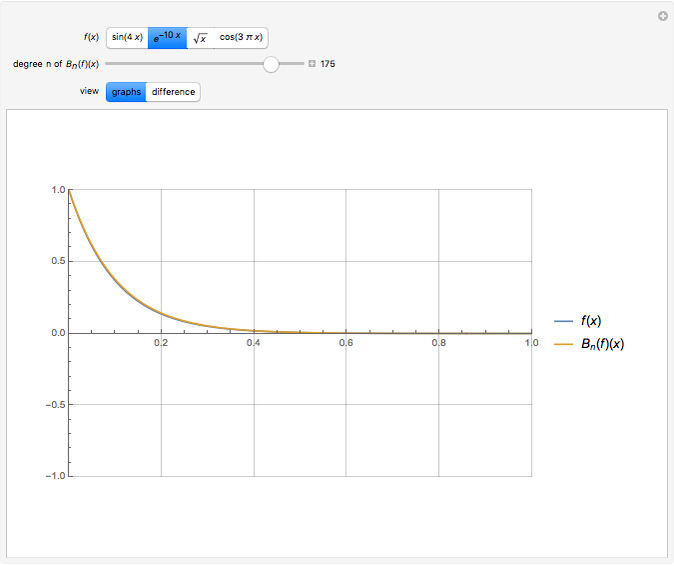
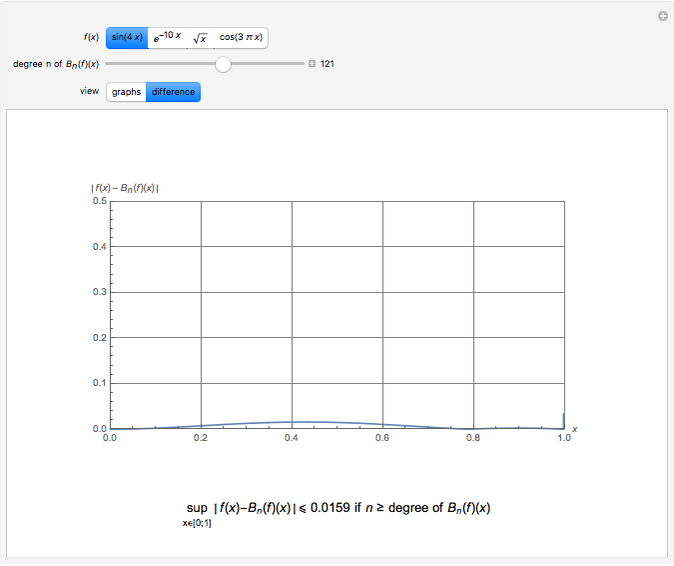
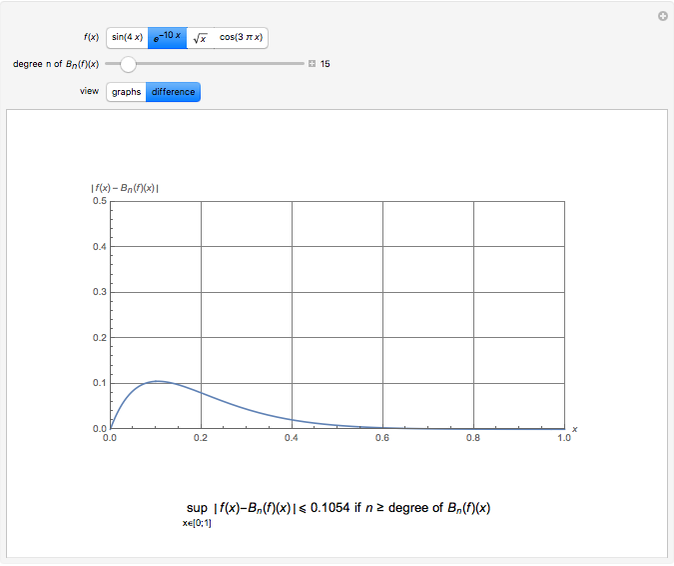
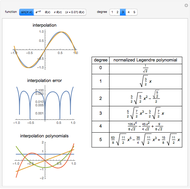
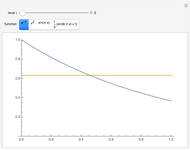
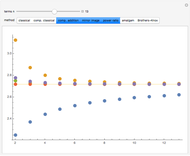
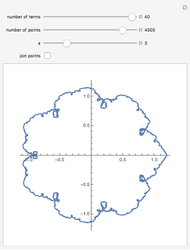
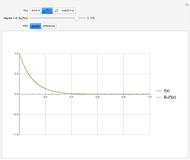
The Weierstrass approximation theorem states that polynomials are dense in the set of continuous functions. More explicitly, given a positive number and a continuous real-valued function 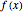defined on , there is a polynomial 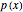such that . Here 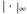is the infinity (or supremum) norm, which in this case (because the closed unit interval is compact) can be taken to be the maximum. The proof of the theorem is based on Bernstein polynomials constructed from , .