A 1D Random Walk with Fractal Dimension 2.0

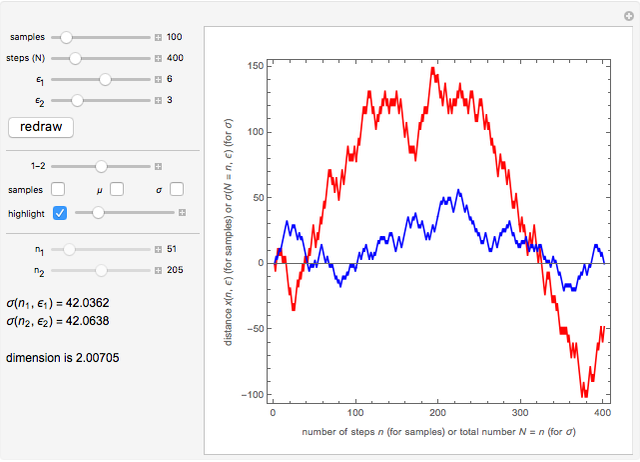
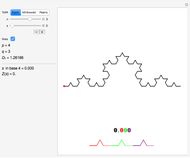
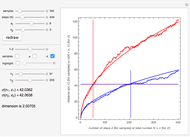
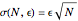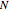This Demonstration illustrates the random walk property where is the dispersion, is the number of steps, and is the size of a step. The relation 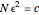, a constant, is here shown to be the signature of a fractal dimension equal to 2.

The fractal dimension of an object is the power that links the number 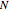of smaller objects used to measure it and their typical length , which is called the resolution.

When 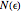is known, then the fractal dimension 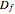is by definition 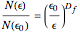, where 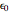is an arbitrary resolution of reference. It can be written 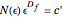(the constant 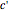is fixed by the arbitrary chosen reference 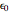). The object of reference might be chosen to be the whole main object itself, so that , , and the definition becomes .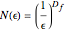

Once this law is known, any dimensional measure of the object can be computed: length in 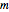, surface in , volume in , "Koch-measure" in 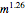, or any 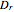measure in 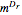, where 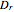is a dimension of reference (the fractal dimension of the measuring object). In general, the 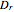measure is only finite when ; it tends to 0 when 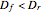and to 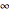when 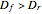(e.g., a Koch curve has infinite length, null surface, and constant "Koch-measure" measured in 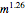). The general law is given by 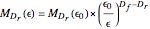, where 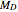is the measure. As 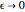, it is clear that the sign of gives the limit of the measure (0, constant, or infinite). In other words, at infinite resolution, an object has a finite, non-null measure only when measured in its own (fractal) dimension.

In the case of the usual self-similar fractals, the relation 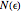is given recursively by the generator of the fractal, for instance 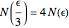for the Koch curve, which, once paired with the definition of 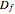, , 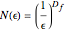gives 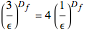and hence .

But the case of a random walk is different because it is a nondeterministic process, so there is no generator and the curve is not even unique. Nevertheless, it is possible to get the needed relation 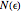by statistical means: it is the very definition of the dispersion 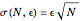. It then becomes possible to get the dimension of a random curve statistically. The hidden order lies in the rules used to generate the walk: equal probability for each direction and independence of each trial (Markov process).

Here, the needed relation is obtained by imposing that 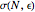is constant, which amounts to fixing a reference object , for example, the distance between two fixed points. This is consistent with the meaning of the dispersion 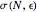, which is the mean departure away from the mean value (here ) and can be thought of as the mean displacement of the drunken sailor. That 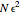is constant can now be understood as the signature of a fractal dimension 2.

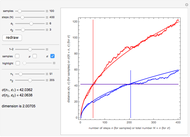
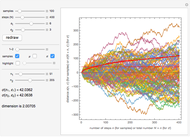
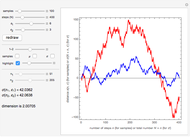
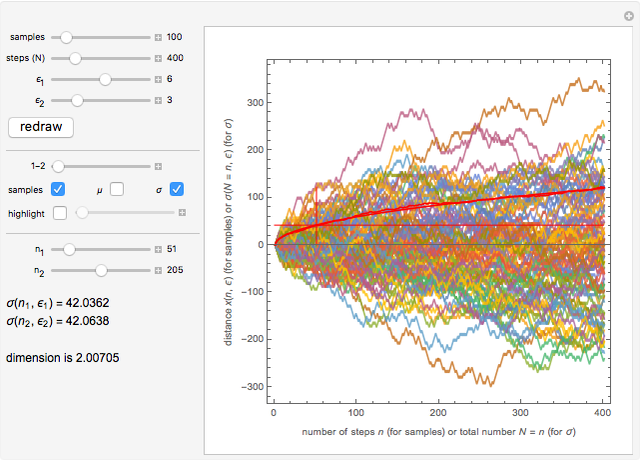
In this Demonstration, two sets of random walks with two different resolutions (step sizes) and 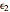are computed with their statistical properties and .

You can choose the number of samples, the number 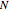of steps, and the two resolutions and 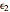. The "redraw" button recomputes new samples with the new chosen values. You can display all the samples (large numbers of samples or steps may be slow on some computers), the mean functions (with their theoretical value: ), and the functions (with their theoretical values: ).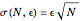

The 1-2 slider lets you choose to look at only one set or both and the "highlight" checkbox highlights one sample that you can select with the corresponding slider (this may help to compare individual samples with different resolutions).

When adjusting the sliders 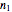and 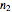so that , you can check that the computed dimension 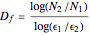is around 2, with an error depending on how far the experimental 's are from their theoretical values (the more samples, the smaller the error).

The intuitive meaning of all this is that when you compare two random walks at two different resolutions (between two fixed points, here and 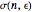), each step contains (on average) 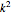steps times smaller. You need four small steps to make one step two times larger, nine small steps to make one step three times larger, and so on. 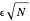Another way to see it is to consider the displacement as a new step of size , which contain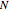s steps , but is only times larger.

If the fractal dimension of the random walk is unknown from theory, this Demonstration lets you retrieve it by numerical experiment.

Understanding fractal dimensions and fractal functions is particularly important in the light of Laurent Nottale's scale relativity [1], where the spacetime coordinates are functions of their resolutions (and hence are fractal curves). The dimension 2 is especially important, as it has been shown (first by Feynman [2]) that each (fractal) spacetime coordinate acquires dimension 2 at the quantum scale.

References

[1] L. Nottale, Scale Relativity and Fractal Space-Time, London: Imperial College Press, 2011.

[2] R. Feynman and A. Hibbs, Quantum Mechanics and Path Integrals, New York: McGraw–Hill, 1965.