Parametrization of a Fractal Curve

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
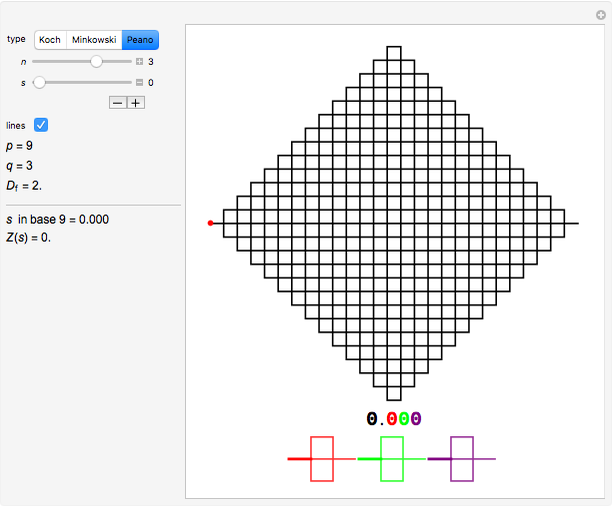
The shown parametrization of some well-known fractal curves is interesting because the values of the parameters reflect the hierarchy of the curves.
Contributed by: Cedric Voisin (August 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
A self-similar fractal is constructed by recursively applying a given generator at smaller and smaller scales. Start with a segment, apply the generator to this segment, then apply the generator to every new smaller segment, and so on.
This sort of fractal exhibits a simple hierarchy in which the same shape repeats itself at every discrete scale.
If the generator contains 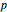 points, then you can use a number
points, then you can use a number 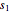 , with
, with  , to localize a point on this generator.
, to localize a point on this generator.
Applying this procedure recursively  times, you can locate any point of the fractal with a list of
times, you can locate any point of the fractal with a list of  numbers
numbers 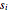 (with
(with 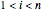 ) giving the position of each new generator at the first
) giving the position of each new generator at the first  scales of the fractal:
scales of the fractal: 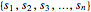 .
.
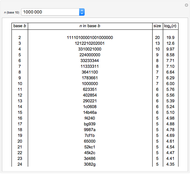
Writing these  digits in a row, you end up with a number
digits in a row, you end up with a number  written in base
written in base 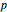 and containing
and containing  digits:
digits:
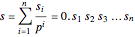 .
.
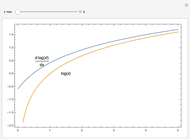
Thus  is a parameter between 0 and 1 that can have an infinite number of places in base
is a parameter between 0 and 1 that can have an infinite number of places in base 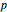 (as
(as  ) and which uniquely specifies any point on the fractal curve. This can be used as a curvilinear coordinate for the fractal, so that it is possible to write the fractal as a set of complex numbers
) and which uniquely specifies any point on the fractal curve. This can be used as a curvilinear coordinate for the fractal, so that it is possible to write the fractal as a set of complex numbers  parametrized by
parametrized by  :
:
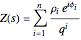 , where
, where 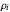 and
and 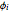 are functions of the geometric properties of the generator (see [1] for details).
are functions of the geometric properties of the generator (see [1] for details).
Hence the equality 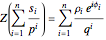 :
:
• shows the analogous roles played by 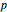 and
and  respectively for the parameter
respectively for the parameter  (as the base of the number) and the complex number
(as the base of the number) and the complex number  (as the resolution of the curve);
(as the resolution of the curve);
• exhibits simultaneously the hierarchical structure of both (real and complex) structures; and
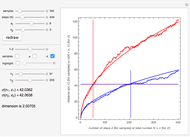
• gives a meaning to the fractal dimension 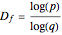 as the ratio of the amounts of information contained in both descriptions of the fractal (real
as the ratio of the amounts of information contained in both descriptions of the fractal (real  and complex
and complex 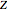 ) at each scale.
) at each scale.
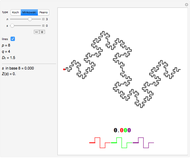
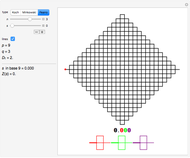
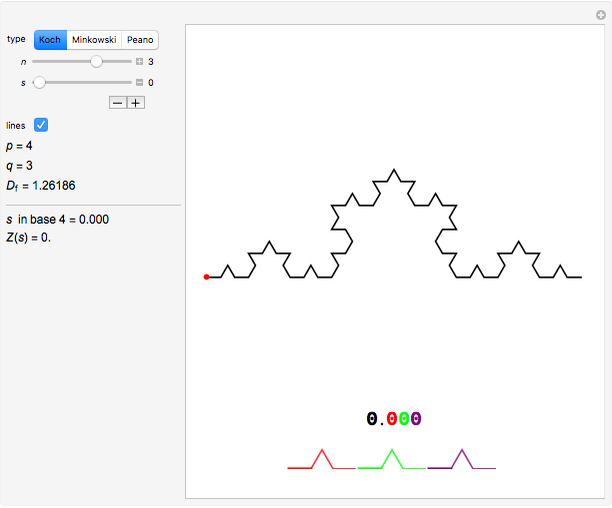
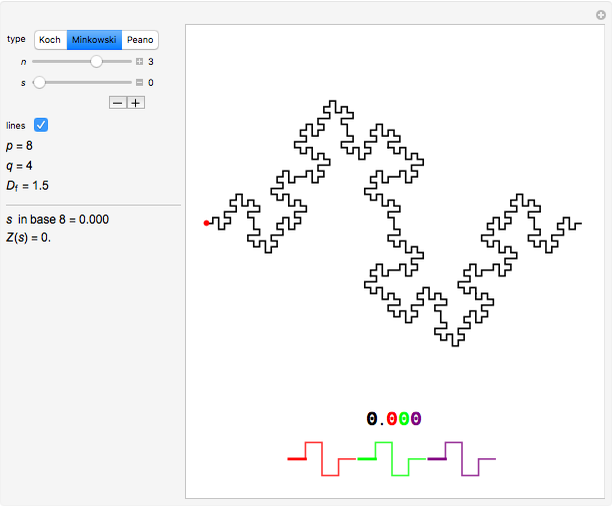
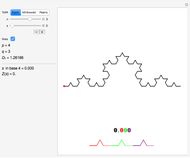
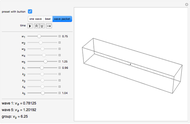
This Demonstration illustrates this construction for three standard fractal curves.
You can choose the fractal among these three classic curves (the fractal dimension 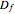 is given), choose the level
is given), choose the level  of recursion, and then move the red point
of recursion, and then move the red point  by varying the parameter
by varying the parameter  .
.
The fractal is actually composed of points only, and the segments are merely conventional ways of joining the points at a finite scale. You can choose not to draw them with the "lines" checkbox, giving the fractal the appearance of a cloud of points.
The parameter  is displayed twice:
is displayed twice:
• in black on the left as a regular number expressed in a base 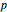 that depends on the chosen fractal, and
that depends on the chosen fractal, and
• in color on the picture, where each digit is colored according to the scale it represents.
This parametrization is important in the framework of scale relativity [1,2], in which the quantum behavior is retrieved by abandoning the hypothesis of a differentiable space-time. A space-time geodesic at quantum scale becomes fractal and  is its proper time. See [1] for a detailed study of this parametrization.
is its proper time. See [1] for a detailed study of this parametrization.
References
[1] L. Nottale, Fractal Space-Time and Microphysics: Towards a Theory of Scale Relativity, Singapore: World Scientific, 1993.
[2] L. Nottale, Scale Relativity and Fractal Space-Time: A New Approach to Unifying Relativity and Quantum Mechanics, London: Imperial College Press, 2011.
Permanent Citation