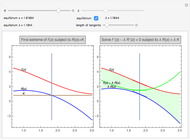
Continuous Changes in Self-Similar Fractals

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
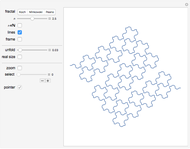
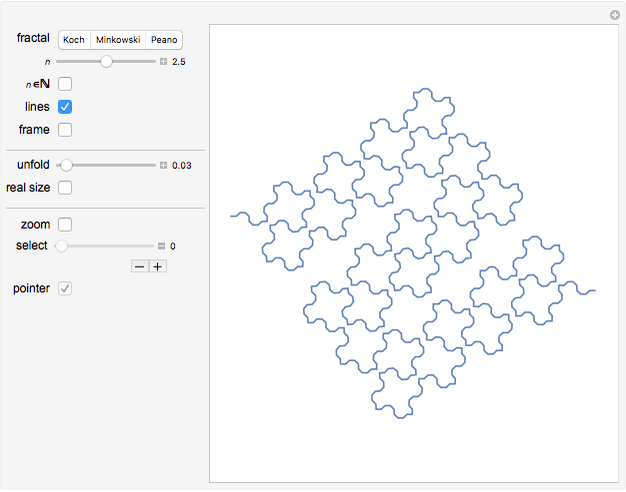
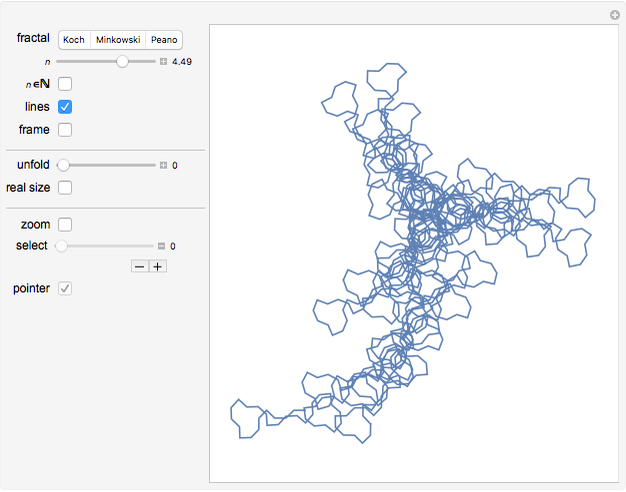
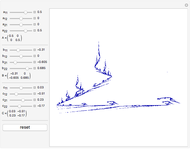
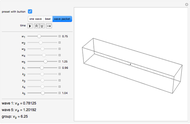
This Demonstration constructs three classic self-similar fractals with a linear interpolation between the usual discrete steps, allowing a continuous variation of some parameters, including the resolution.
Contributed by: Cedric Voisin (January 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This Demonstration draws self-similar fractals using linear interpolation between the usual discrete steps, which allows continuous deformation of the fractals by varying the resolution.
This Demonstration illustrates some possible uses of such a construction.
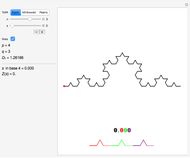
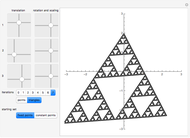
For the three classic self-similar fractals (Koch curve, Minkowski sausage, and Peano curve), you can continuously modify the level of recursion  . You can get the standard discrete variation by checking the
. You can get the standard discrete variation by checking the 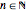 checkbox.
checkbox.
A tooltip on the fractal buttons gives the values of 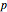 and
and  .
.
The straight lines are merely a conventional way to join the points at finite resolution; they do not belong to the fractal and you can suppress them.
You can display the frame whenever needed.
If you do not check the real size box, the scale is permanently adjusted for the fractal to occupy the maximum possible space in the graphic.
If you check the real size box, the whole sequence of unfolding is displayed at constant scale. This shows how the proper length of a fractal increases with its level of recursion. Its length increases like 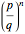 , as you can see by displaying the frame.
, as you can see by displaying the frame.
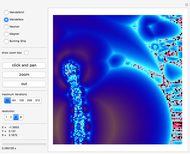
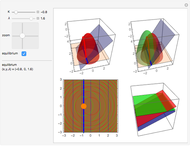
Zoom Options
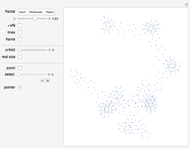
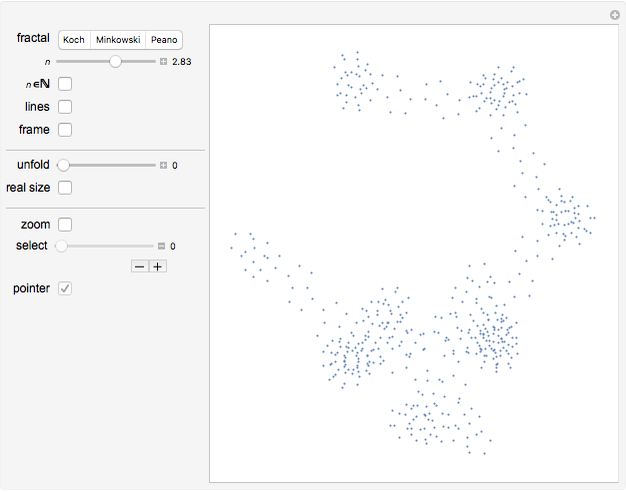
The select slider lets you select the center of the zoom, which can be displayed with the pointer checkbox. A tooltip on the slider gives the coordinates of the zoom.
The plot range has to be adjusted so that the  level gives the same picture as the
level gives the same picture as the  level. In other words, the range has to compensate the variation of the resolution
level. In other words, the range has to compensate the variation of the resolution 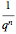 and must vary as
and must vary as 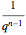 so that the length of the segments remains apparently constant (with value
so that the length of the segments remains apparently constant (with value  ) each time
) each time  increases by 1, giving the impression of a zoom linear with
increases by 1, giving the impression of a zoom linear with  .
.
In a sense, the plot range 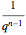 is our measurement resolution, while the length of the segments
is our measurement resolution, while the length of the segments 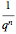 is the resolution of the fractal. The ratio of the two (the measurement process) is the constant apparent resolution
is the resolution of the fractal. The ratio of the two (the measurement process) is the constant apparent resolution  .
.
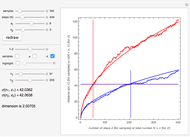
The key point here is that it illustrates how the logarithm of the resolution (here  ) is the most relevant quantity to measure a change of resolution.
) is the most relevant quantity to measure a change of resolution.
It also gives the interesting equivalence for ways of seeing  intuitively:
intuitively: 
 level of recursion
level of recursion  logarithm of resolution
logarithm of resolution  information content.
information content.
See the Demonstrations Parametrization of a Fractal Curve and Logarithm Seen as the Size of a Number by the same author for more details about this equivalence.
The zoom viewpoint is remarkable as it highlights the following features:
• The self-similarity of discrete fractals is a particular case of log periodicity (the shape of the structure repeats itself only for discrete differences of the log of the resolution).
• The logarithm  of the resolution appears as a fundamental way of describing a change of scale.
of the resolution appears as a fundamental way of describing a change of scale.
References
[1] L. Nottale and J. Schneider, "Fractals and Nonstandard Analysis," Journal of Mathematical Physcs, 25(5), 1984 pp. 1296–1300. doi:10.1063/1.526285.
[2] L. Nottale, Fractal Space-Time and Microphysics: Towards a Theory of Scale Relativity, Singapore: World Scientific, 1993.
Permanent Citation