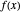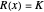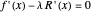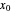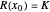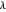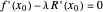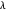Details

The formal idea of the Lagrange multipliers is to replace the problem of finding the extremum of a function 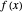with a constraint 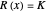, where 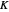is a constant, with the problem of finding critical points of the function 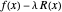subject to the same constraint.

Of course, in 1D, the Lagrange multiplier technique is useless, as the solution is trivially given by solving the constraint 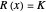, whatever the function 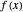may be. Nonetheless, the 1D view, trivial as it may be, provides everything that is needed to understand the geometrical meaning of the Lagrange multiplier.

Indeed, it can be seen that is nothing but a rescaled 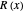, and that the function 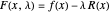is nothing but the difference in height between 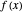and 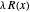. When both functions are parallel, the difference is constant, giving the solution of the problem.

This height difference 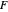can be understood as a new potential in a nonequilibrium (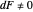) or equilibrium (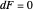) state.

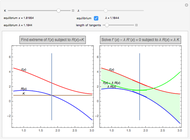
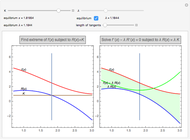
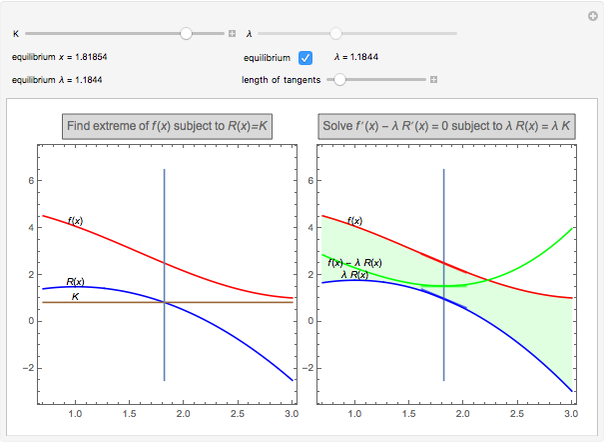
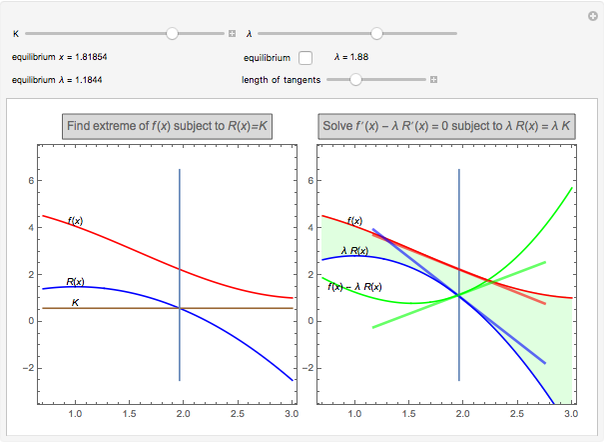
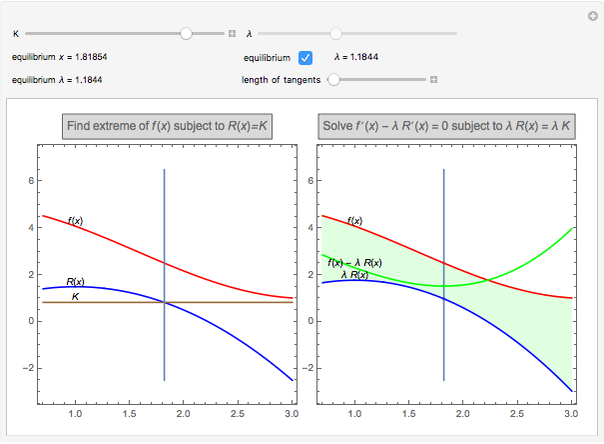
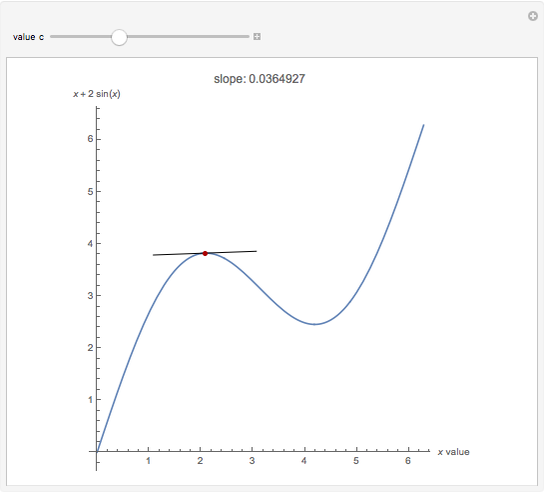
A few explanations about both graphs follow.

The graph on the left is the original problem (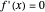 and ).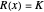

The graph on the right is the problem solved with a Lagrange multiplier (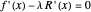 and 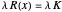). The height of the green curve is the green area. The thick lines are the tangents to the three functions. You can change their length with the slider to check the red and blue tangents are parallel and the green tangent is horizontal.

When modifying the constraint 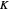, the Lagrange multiplier is computed (equilibrium 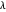), but the interactive (nonequilibrium) value of 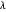can be modified to get the feeling of its meaning. The key point is that when 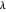varies, it modifies the slope of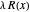 everywhere (by rescaling 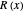), and the equilibrium value is the one that compensates for the variation (which, in the 2D case, will restore the 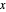- 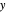independence).

It is interesting to note that, when choosing , 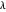takes the for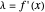m (from 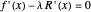), and the new potential is the Legendre transform of .

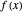As an example, in statistical mechanics, the temperature 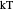is the inverse of a Lagrange multiplier 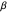that arises when one wants to optimize the number of states given the global constraint 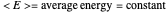. This gives to 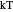the meaning of a natural scale unit for an energy-constrained statistical system.

Another example is given by the thermodynamical potentials that appear here as constrained minimized energies.

In this formalism, the Lagrange multiplier is nothing but a scale (mathematical viewpoint) and dimensional (physics viewpoint) factor. Its physical meaning is that of a "number of thing to minimize per unit constraint": .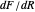

Since the value of the Lagrange multiplier is determined by the constraint, it is interesting to note that a natural scale arises from any optimization with a global constraint. For instance, the temperature 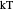(natural scale unit energy of the system) is a direct consequence of the global constraint .

Seeing the Lagrange multiplier as a scaling factor can be of some interest in the paradigm of Laurent Nottale's scale relativity, where the scales become fundamental coordinates of any physical description.

The 2D treatment adds more subtle ideas but is more complex to visualize. Hence it is the subject of a second Demonstration.