A Chain of Tangent Circles

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
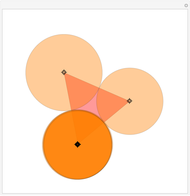
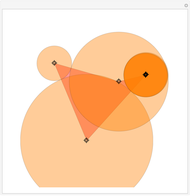
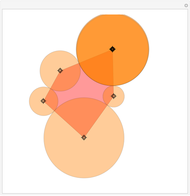
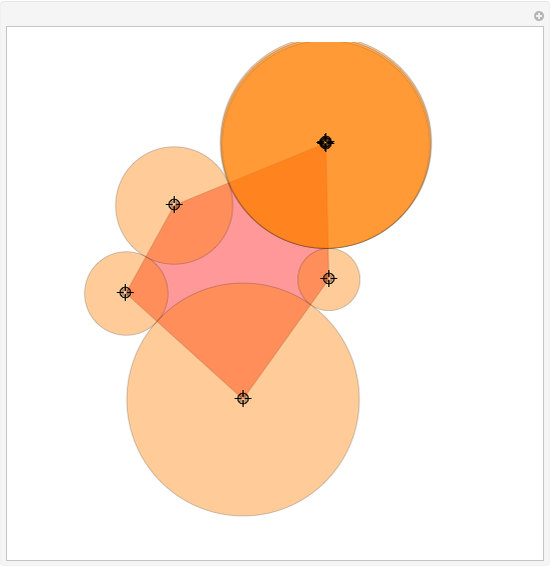
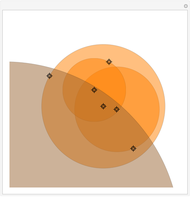
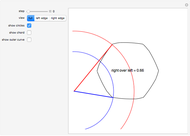
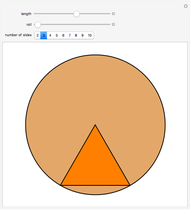
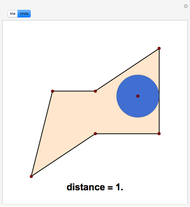
Given any polygon with  vertices, it is possible to draw circles with centers at its vertices so that each circle is tangent to its two neighbors, forming a necklace of circles. If
vertices, it is possible to draw circles with centers at its vertices so that each circle is tangent to its two neighbors, forming a necklace of circles. If  is odd, there is a unique solution; if
is odd, there is a unique solution; if  is even, either there is no solution or an infinite number of solutions. This Demonstration assumes
is even, either there is no solution or an infinite number of solutions. This Demonstration assumes  , but by superimposing circles, solutions for smaller
, but by superimposing circles, solutions for smaller  can be displayed.
can be displayed.
Contributed by: Jaime Rangel-Mondragon (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"A Chain of Tangent Circles"
http://demonstrations.wolfram.com/AChainOfTangentCircles/
Wolfram Demonstrations Project
Published: March 7 2011