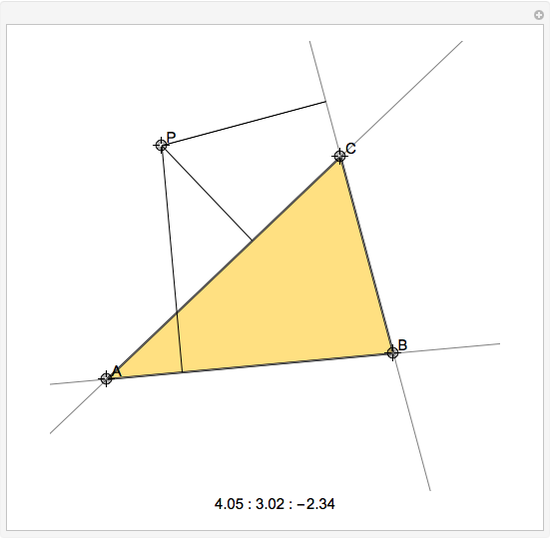
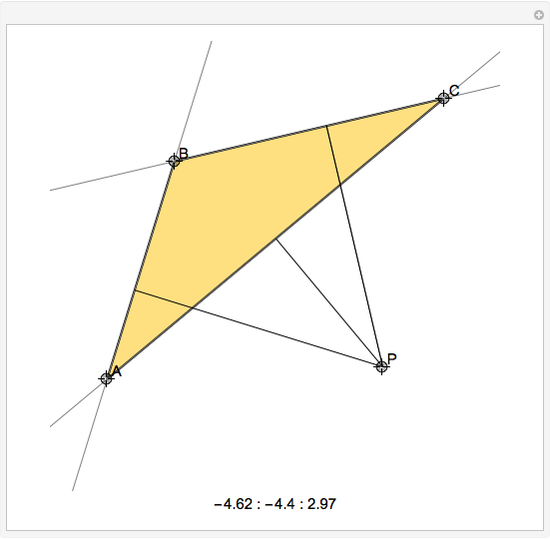
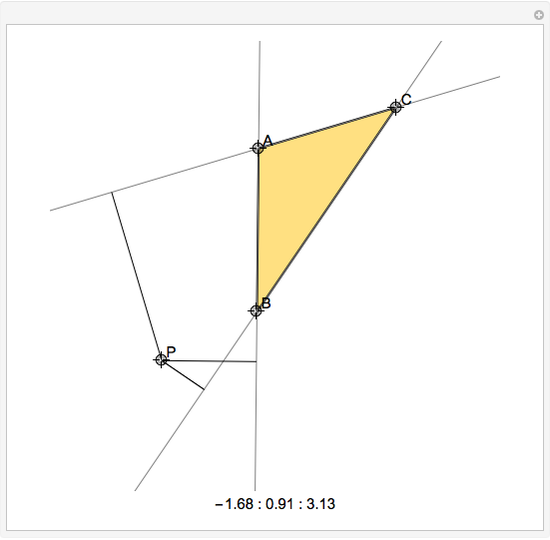
Exact Trilinear Coordinates

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
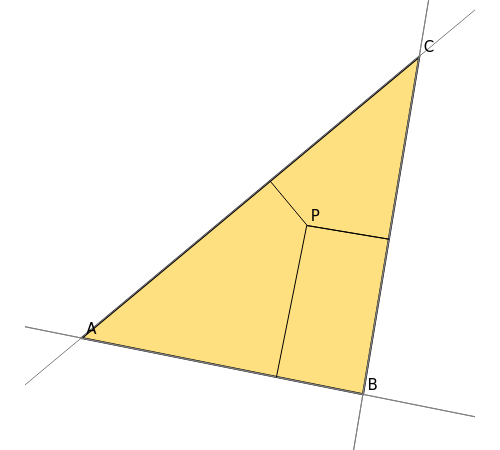
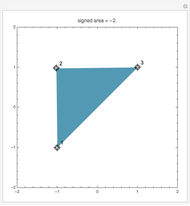
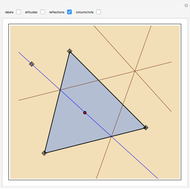
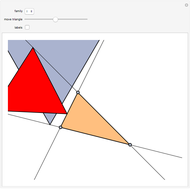
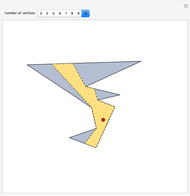
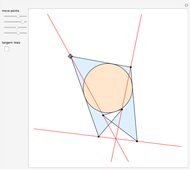
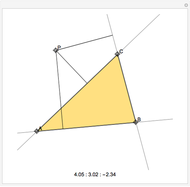
Given a reference triangle 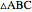 , the trilinear coordinates of a point
, the trilinear coordinates of a point 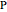 with respect to that triangle is any ordered triple of numbers proportional to the directed distances from
with respect to that triangle is any ordered triple of numbers proportional to the directed distances from 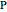 to the directed sides (or their extensions as infinite directed lines)
to the directed sides (or their extensions as infinite directed lines) 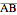 ,
, 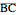 , and
, and 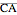 , in that order. Exact trilinear coordinates are trilinear coordinates normalized to be the actual distances of
, in that order. Exact trilinear coordinates are trilinear coordinates normalized to be the actual distances of 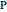 to each of the three sides. The sign of a distance is taken as positive if
to each of the three sides. The sign of a distance is taken as positive if 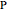 is on the same side of the directed triangle as the triangle and negative otherwise. You can drag the vertices to modify the triangle and the point
is on the same side of the directed triangle as the triangle and negative otherwise. You can drag the vertices to modify the triangle and the point 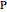 .
.
Contributed by: Jaime Rangel-Mondragon (July 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Exact Trilinear Coordinates"
http://demonstrations.wolfram.com/ExactTrilinearCoordinates/
Wolfram Demonstrations Project
Published: July 17 2014