Brianchon's Theorem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
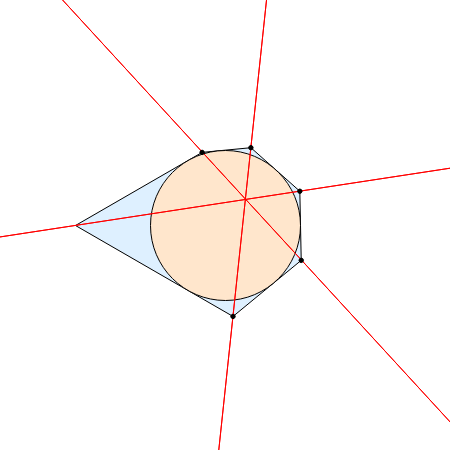
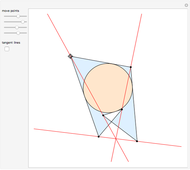
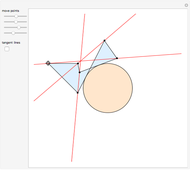
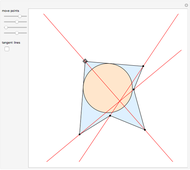
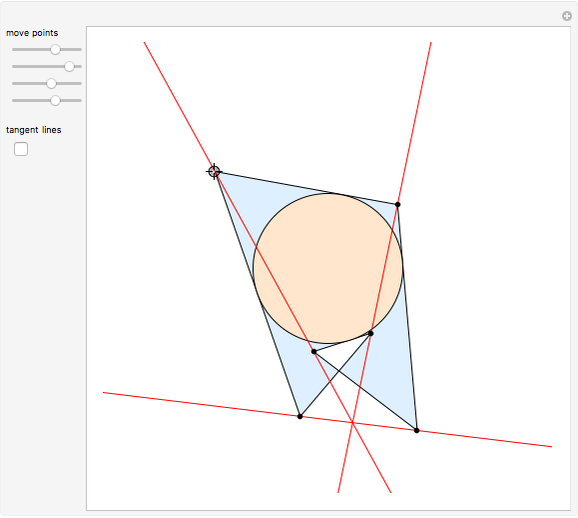
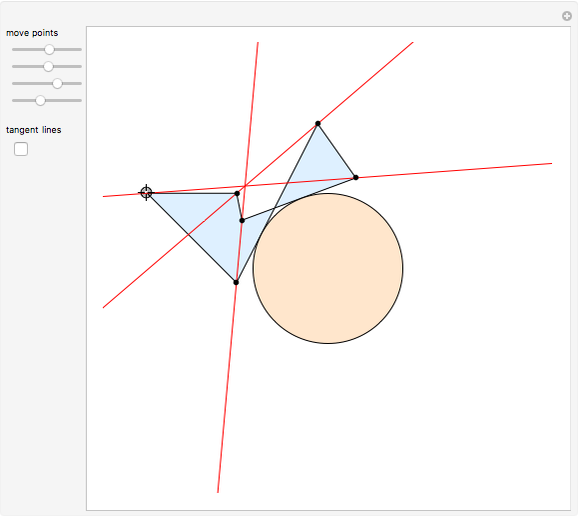
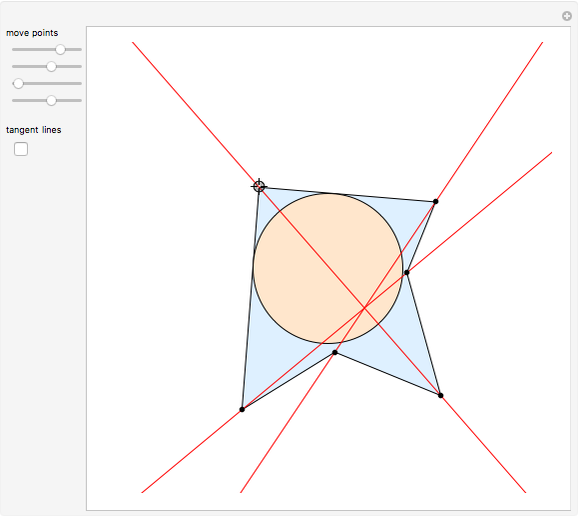
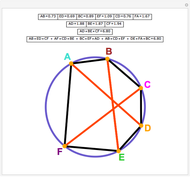
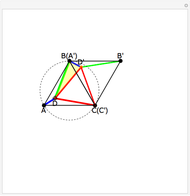
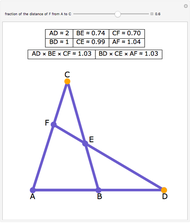
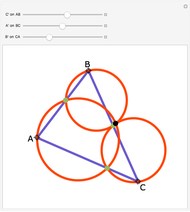
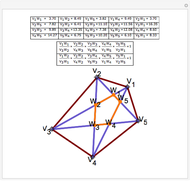
Brianchon's theorem was published in 1810 by the French mathematician Charles-Julien Brianchon (1783–1864). The theorem asserts that if a hexagon is circumscribed about a circle, then the lines joining the opposite vertices are concurrent. This Demonstration shows that the hexagon is considered to circumscribe the circle if each edge, possibly extended, is tangent to the circle. You can use the sliders or drag one of the vertices to vary the hexagon, which can self-intersect, be outside the circle it circumscribes, or both!
[more]
Contributed by: Jaime Rangel-Mondragon (July 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Brianchon's Theorem"
http://demonstrations.wolfram.com/BrianchonsTheorem/
Wolfram Demonstrations Project
Published: July 21 2014