A Proof of the Difference Identity for Cosine

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
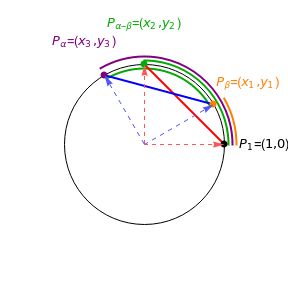
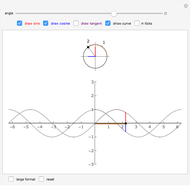
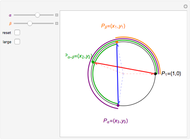
The key observation in the proof of the difference identity for cosine 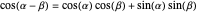 can be shown and investigated with this Demonstration.
can be shown and investigated with this Demonstration.
Contributed by: Eric Schulz (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
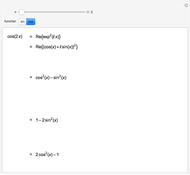
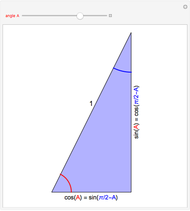
Difference Formula for Cosine
For any two angles 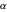 and
and 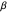 ,
,

Proof
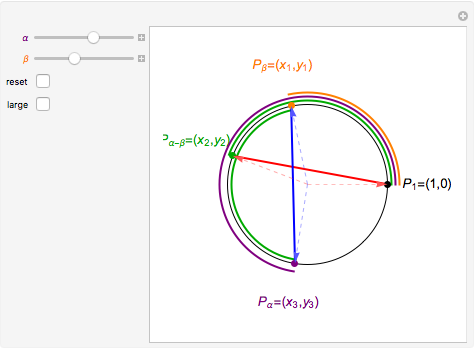
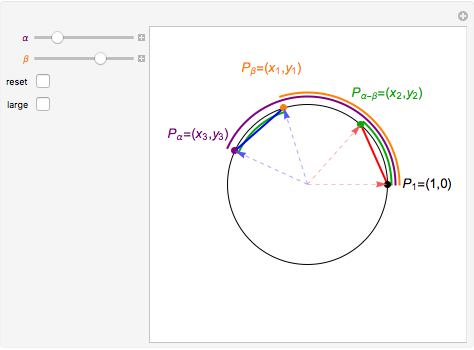
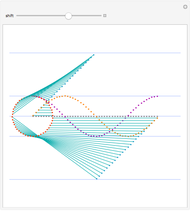
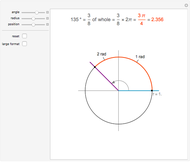
Without loss of generality, assume that 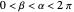 . Plot the points
. Plot the points  ,
, 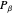 ,
, 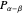 , and
, and  on the unit circle where
on the unit circle where
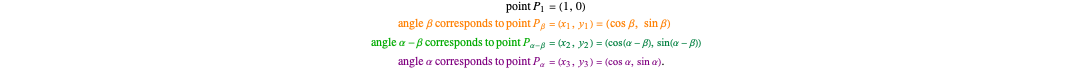 Since the arcs
Since the arcs 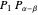 and
and  have the same length, the line segments
have the same length, the line segments 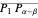 and
and 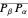 must also have the same length. Experiment with the controls until this statement is understood and use it to investigate how the lengths of the two line segments change, but always remain equal to each other, for different values of
must also have the same length. Experiment with the controls until this statement is understood and use it to investigate how the lengths of the two line segments change, but always remain equal to each other, for different values of 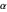 and
and  .
.
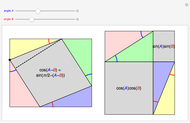
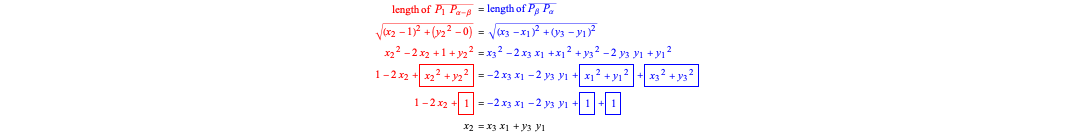 Finally, finish the proof by replacing
Finally, finish the proof by replacing  ,
, 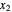 ,
, 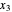 ,
, 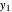 , and
, and  with
with 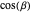 ,
, 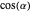 ,
, 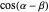 ,
, 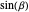 , and
, and 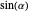 respectively.
respectively.
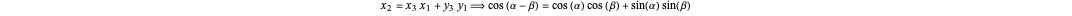
Permanent Citation