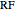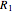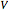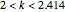Active Negative Resistance Model That Is Not Piecewise Linear

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
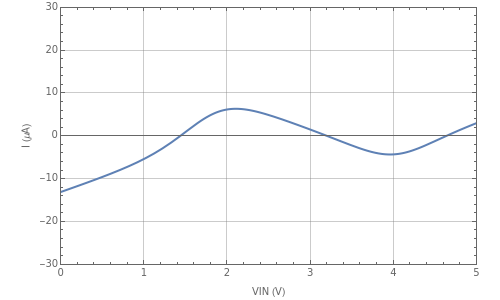
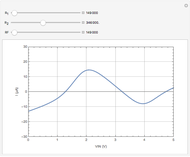
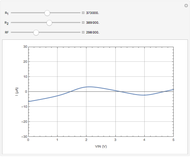
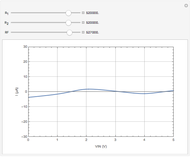
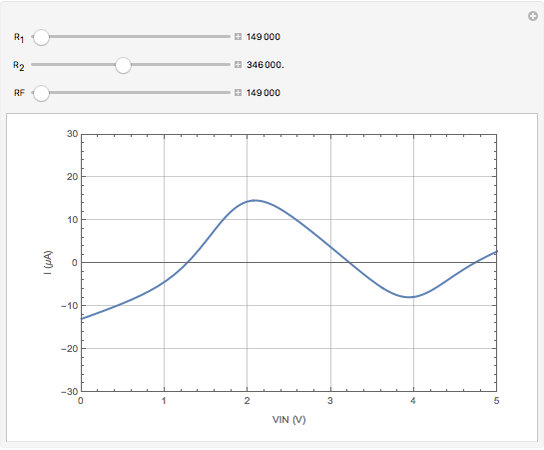
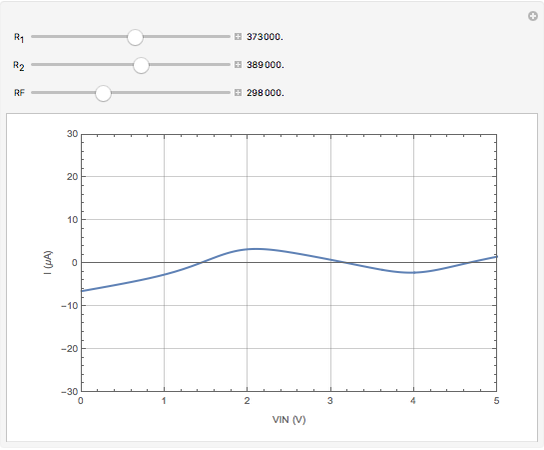
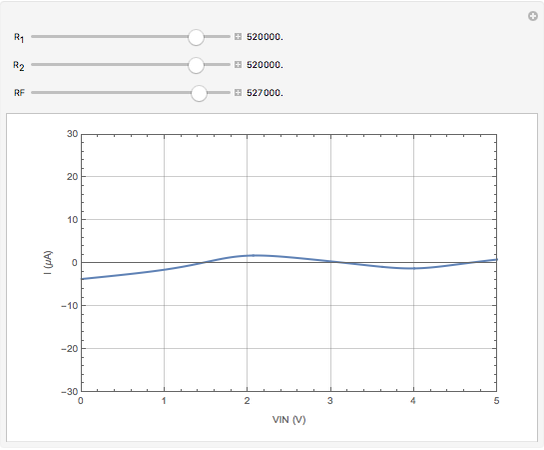
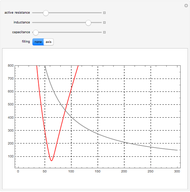
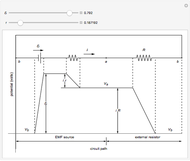
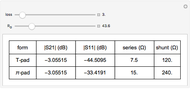
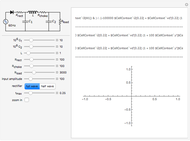
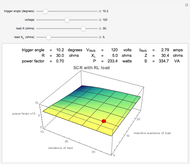
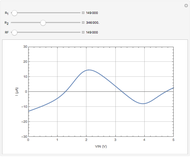
This Demonstration models an operational-amplifier (opamp) based negative resistance (NR) implementation. Traditionally, negative resistance has been modeled with piecewise linear (PWL) equations. This model, however, is continuous and differentiable at all points.
[more]
Contributed by: Isaac Abraham (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] V. Drogoreanu and D. Vizireanu, "A Class of MOS Non-Linear Negative Resistance Oscillators," International Symposium on Circuits and Systems (ISCAS) '96, 3, May 1996, pp. 225–228.
[2] D. N. Vizireanu, "A New Class of MOS Transistor Nonlinear Negative Resistance Oscillators," Electrotechnical Conference, 1996, 1, May 1996, pp. 407–410.
[3] D. N. Vizireanu, et al., "A New Class of S-Type Current Controlled Nonlinear Negative Resistances," International Semiconductor Conference, 2, September 2006, pp. 395–398.
[4] L. O. Chua, C. A. Desoer, and E. S. Kuh, "Linear and Nonlinear Circuits," New York: McGraw–Hill, 1987, pp. 192–195.
[5] L. Shafai, "Analysis of a 2-Terminal Negative Resistance," Electronics Letters, September 1971, pp. 572–573.
[6] Maxim Application Note 815, "Negative-Resistance Load Canceller Allows Voltage Reference to Drive Heavy Loads," September 2001.
Permanent Citation