Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

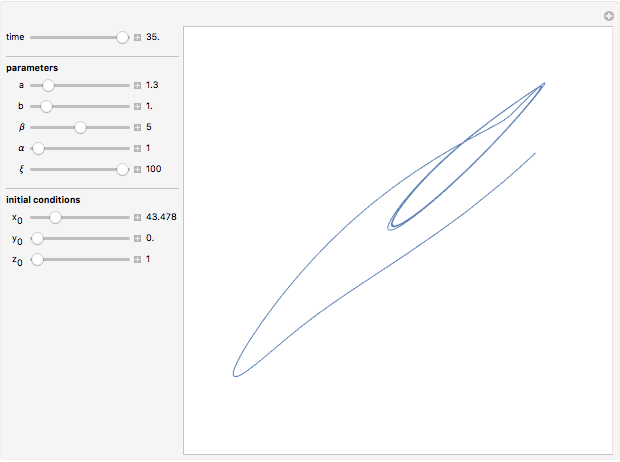
Bifurcation Analysis of a Cubic Memristor Model

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

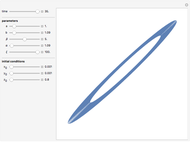
The memristor, named as a contraction for "memory resistor", is supposed to be the fourth fundamental electronic element, in addition to the well-known resistor, inductor, and capacitor. Its theoretical existence was postulated in 1971 by L. O. Chua [1], but its physical realization was announced only recently in a paper published in the May 2008 issue of Nature by a research team from Hewlett–Packard [2]. It has attracted worldwide attention due to its potential applications in the construction of electronic circuits, especially for newer-generation computers.

[more]

In [3] we present a bifurcation analysis of a memristor oscillator mathematical model, given by a cubic system of ordinary differential equations, depending on four parameters.

We show that, depending on the parameter values, the system may present the coexistence of both infinitely many stable periodic orbits and stable equilibrium points.

The periodic orbits arise from the change in the local stability of equilibrium points on a line of equilibria for a fixed set of parameter values. This is an interesting type of Hopf bifurcation, which occurs without varying parameters.

In these graphics we show the birth of periodic orbits by varying the initial conditions and parameters in the model.

[less]

Contributed by: Vanessa Botta, Marcelo Messias, and Cristiane Néspoli (November 2009)
Open content licensed under CC BY-NC-SA

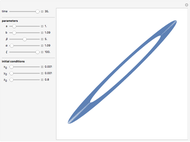
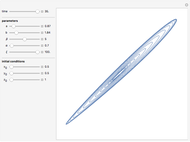
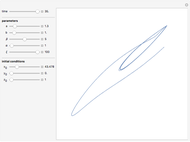
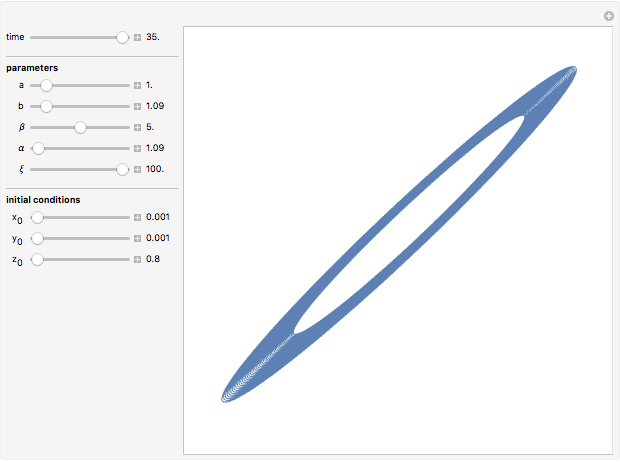
Snapshots

Details

References:

[1] L. O. Chua, "Memristor—The Missing Circuit Element," IEEE Trans. Circuit Theory, 18(5), 1971 pp. 507–519.

[2] D. B. Strukov, G. S. Snider, G. R. Stewart, and R. S. Williams, "The Missing Memristor Found," Nature, 453, 2008 pp. 80–83.

[3] M. Messias, C. Néspoli, and V. Botta, "Hopf Bifurcation from Lines of Equilibria without Parameters in Memristor Oscillators," Internationl Journal of Bifurcation and Chaos (to appear).

Links:

http://www.eecs.berkeley.edu/~chua/circuitrefs.html

http://nonlinear.eecs.berkeley.edu

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send