An Efficient Test for a Point to Be in a Convex Polygon

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
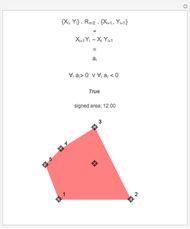
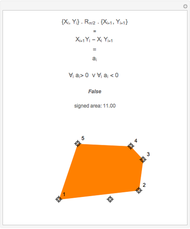
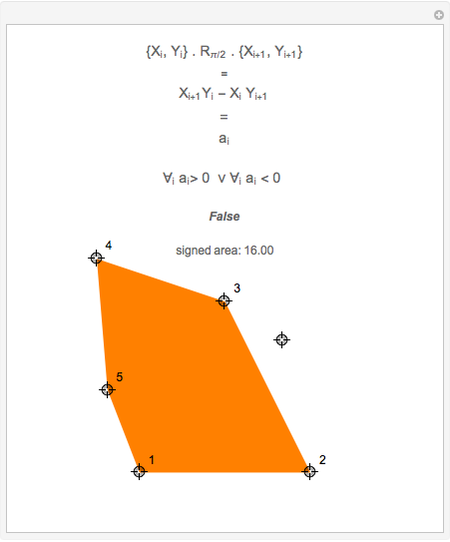
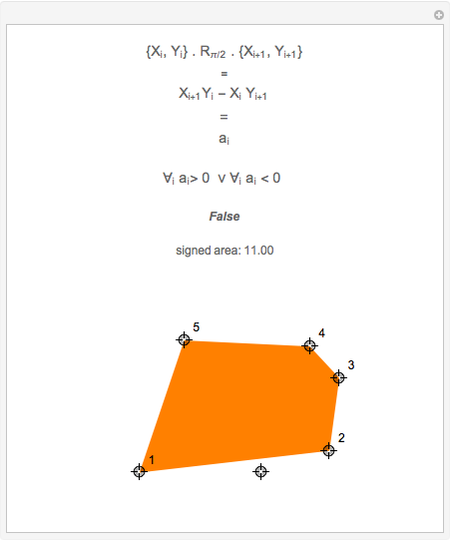
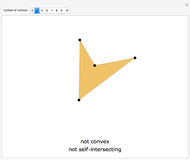
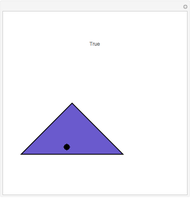
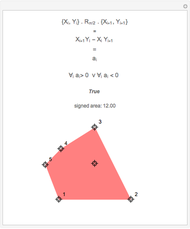
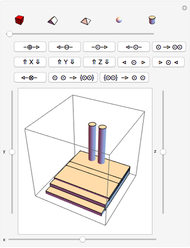
This Demonstration shows an efficient test for checking whether a point is in a convex polygon, indicated by a color change. Note that the test works correctly only for convex polygons.
Contributed by: Robert Nowak (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This simple and efficient algorithm determines whether a point 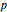 is located inside a convex polygon or not. Suppose the polygon has
is located inside a convex polygon or not. Suppose the polygon has  vertices.
vertices.
First the polygon is translated by 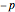 , so that
, so that 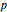 becomes the new origin.
becomes the new origin.
Next the angles of all pairs of adjacent vectors pointing from the origin to the vertices of the polygon are calculated.
If all the angles are in the range  to
to  (when the polygon is defined counterclockwise) or all in
(when the polygon is defined counterclockwise) or all in  to
to  (in the clockwise case), then the point is inside the convex polygon.
(in the clockwise case), then the point is inside the convex polygon.
The angle calculation can be accomplished as follows:
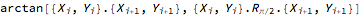 ,
,
where  is the rotation matrix through
is the rotation matrix through 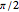 .
.
The dot product with  reverses the
reverses the  ,
,  coordinate values and adjusts one of their signs; it is used so that only arctan and the dot product are needed.
coordinate values and adjusts one of their signs; it is used so that only arctan and the dot product are needed.
Fortunately we only need the Boolean information of the sign of the angle, so the necessary calculation simplifies to
 . This further expands to
. This further expands to  .
.
Note: 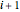 must be treated mod
must be treated mod  .
.
Further we can see that  ; this is the area spanned by the two vectors, giving us the total signed area of the polygon:
; this is the area spanned by the two vectors, giving us the total signed area of the polygon: 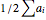 .
.
So the total costs for the test are just two additions (for the initial origin translation), two multiplications, one subtraction, and one "greater than zero" comparison for every vertex; finally an  -fold equality comparison if all the signs of the angles are equal. No floating-point calculations are needed in the case of integer coordinates.
-fold equality comparison if all the signs of the angles are equal. No floating-point calculations are needed in the case of integer coordinates.
Additionally, the signed area of the polygon is calculated to show that both orientations of polygons are handled correctly.
This Demonstration was developed before fully understanding the Point in Triangle Demonstration. The slight difference is the use of the DotProduct (and perhaps a better documentation/explanation and a more compact implementation) in contrast to the Determinant used in Point in Triangle.
Similar algorithms exist which unnecessarily sum up all the mentioned angles (not only their signs), at the relative high costs of arctan and floating-point operations.
Permanent Citation