Sylvester's Four-Point Problem
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
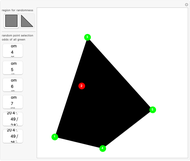
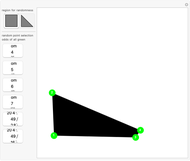
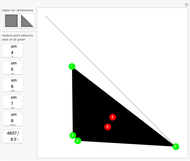
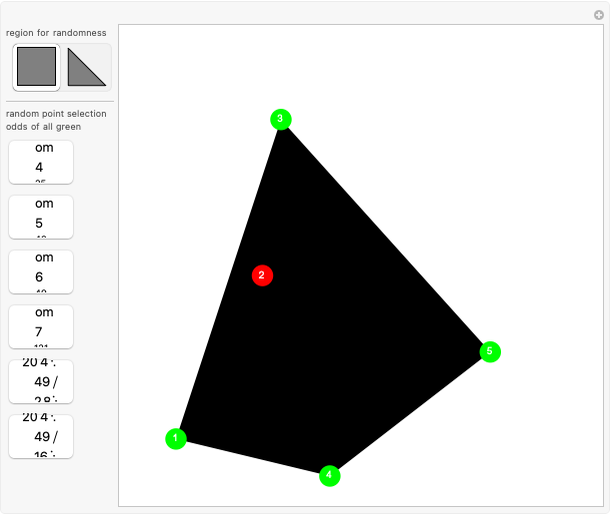
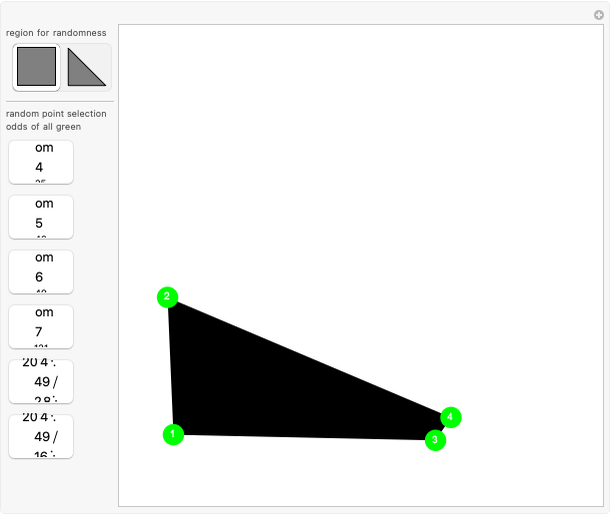
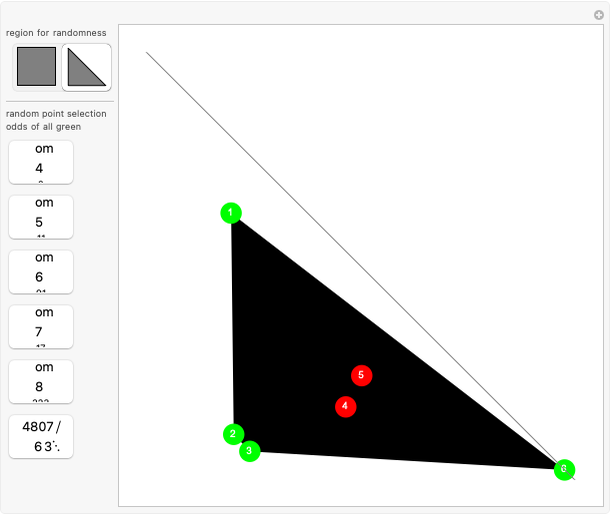
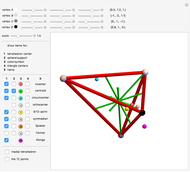
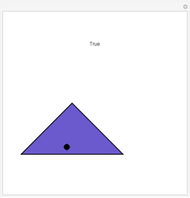
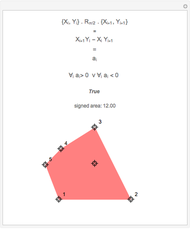
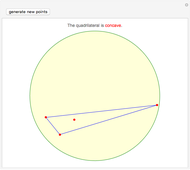
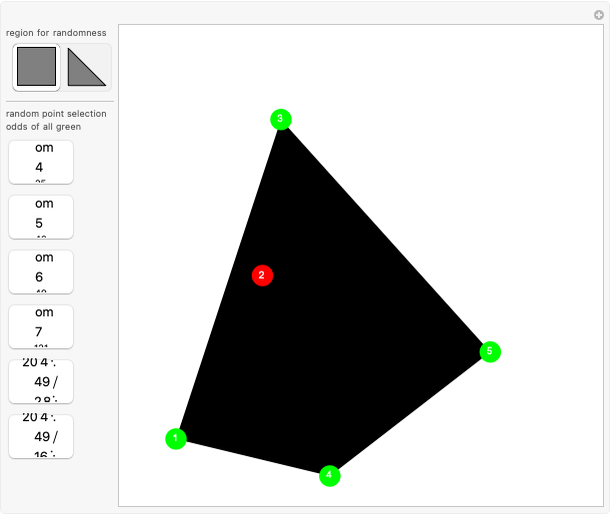
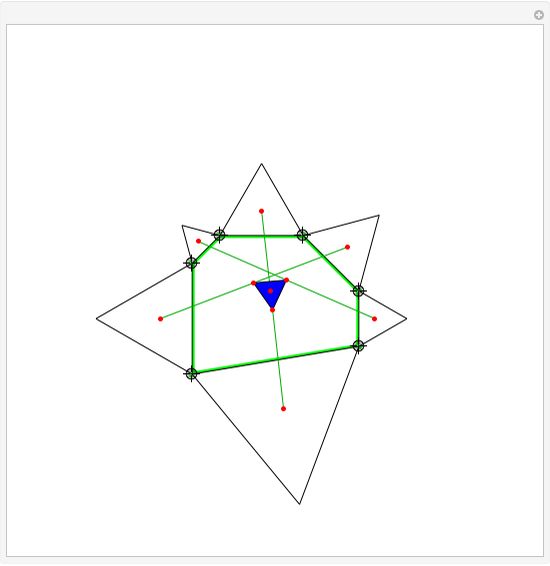
Pick 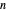 random points from a region, then find the convex hull. What are the odds that all the generating points are on the boundary of the hull? In 1865, Sylvester stated, "This problem does not admit of a determinate solution." Actually, the answer depends on the region. Four points from a triangular region have odds of
random points from a region, then find the convex hull. What are the odds that all the generating points are on the boundary of the hull? In 1865, Sylvester stated, "This problem does not admit of a determinate solution." Actually, the answer depends on the region. Four points from a triangular region have odds of 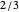 of making a quadrilateral. Four points from a rectangular region have odds of
of making a quadrilateral. Four points from a rectangular region have odds of 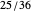 of making a quadrilateral.
of making a quadrilateral.
Contributed by: Ed Pegg Jr (December 2017)
Open content licensed under CC BY-NC-SA
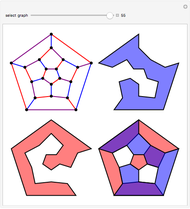
Snapshots
Details
Permanent Citation