Signed Area of a Polygon


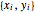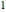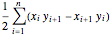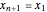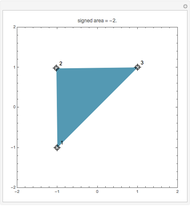
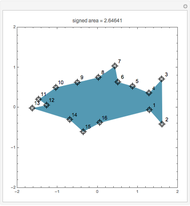
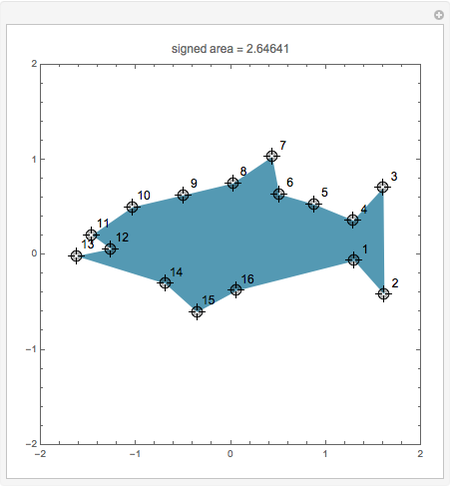
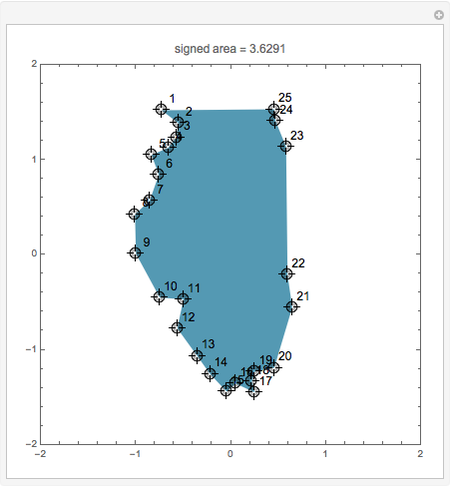
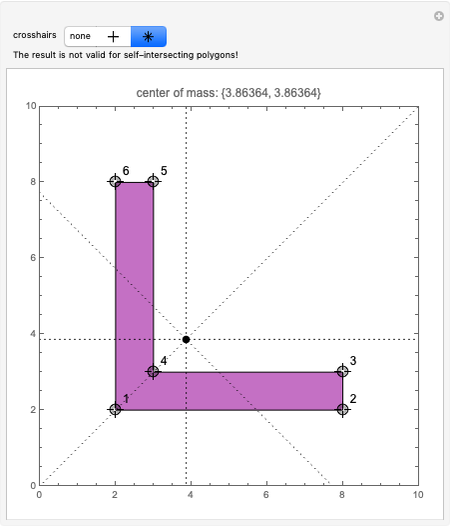
	The signed area of a polygon with vertices numbered through can be calculated exactly by the formula , where and 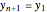. If the polygon is simple (non-intersecting sides), with the vertices numbered in a counterclockwise direction, the signed area is the area. This formula is surprisingly useful in surveying, architecture, and many other applications.


	Contributed by: Bruce Atwood (Beloit College) and Stan Wagon (Macalester College) After work by: Stan Wagon

The formula for the area of a simple polygon can be elegantly derived using Green's theorem and extended to moments of the region.
S. F. Bockman, "Generalizing the Formula for Areas of Polygons to Moments," Amer. Math. Monthly, 96(2), 1989 pp. 131-132.

For more information, see:
S. Wagon, Mathematica in Action, 2nd ed., New York: Springer, 1999.

Polygon Area (Wolfram MathWorld)

Green's Theorem (Wolfram MathWorld)

"Signed Area of a Polygon" from The Wolfram Demonstrations Project
http://demonstrations.wolfram.com/SignedAreaOfAPolygon/

Contributed by: Bruce Atwood (Beloit College) and Stan Wagon (Macalester College)

After work by: Stan Wagon

Free Download: Mathematica Player--Runs all Demonstrations & more

Browse all topics

Source page:

Name (optional)

Occupation (optional)

Organization (optional)

I use Mathematica:

often

occasionally

never

Country (optional)
Remember me

Note: Please do not include anything you consider confidential or proprietary. We will keep your information private. We will not give it to any third party.
Privacy Policy »