Approximation by Orthogonal Polynomials
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
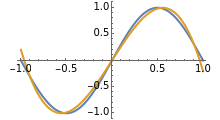
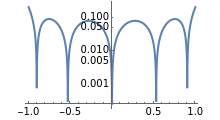
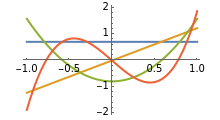
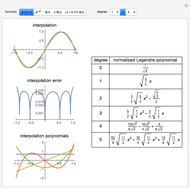
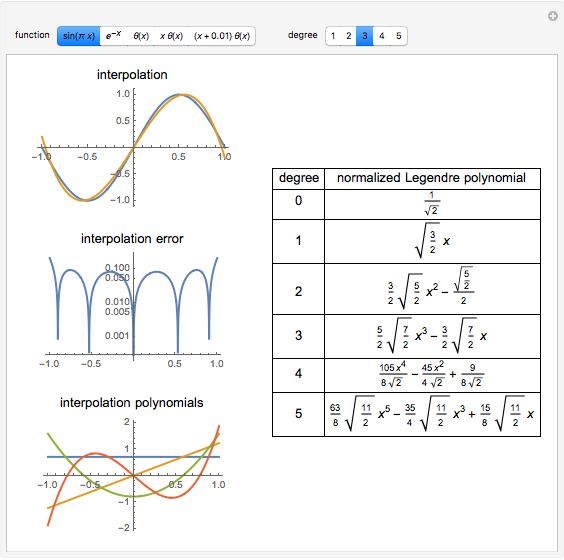
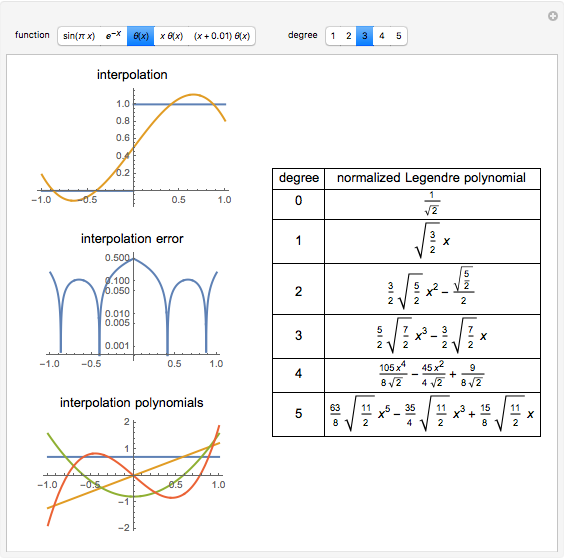
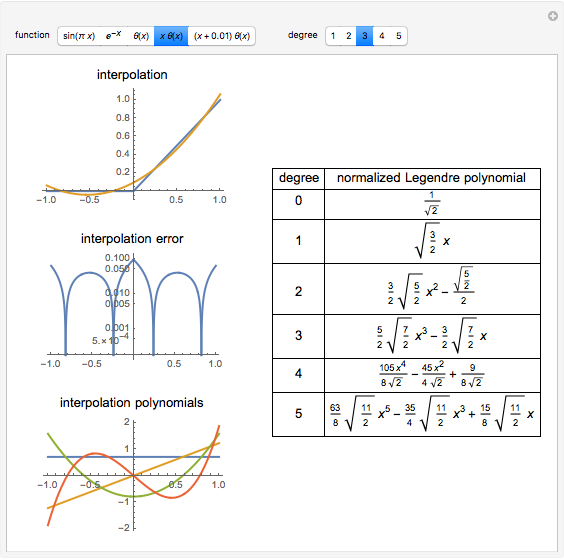
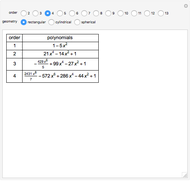
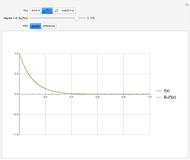
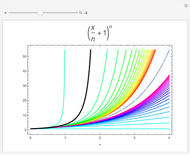
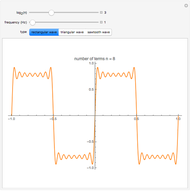
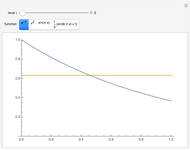
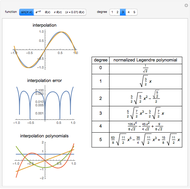
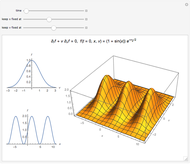
The Gram–Schmidt process is used to obtain orthonormal polynomials with respect to the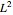 
norm. These polynomials are then used to interpolate a number of functions; a logarithmic error plot is provided.
Contributed by: Lukas Einkemmer (December 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Approximation by Orthogonal Polynomials"
http://demonstrations.wolfram.com/ApproximationByOrthogonalPolynomials/
Wolfram Demonstrations Project
Published: December 16 2013
Bernstein Polynomials and Convex Bézier Sums
Ludwig Weingarten
Orthogonality of Two Functions with Weighted Inner Products
Alain Goriely
Roots of the Bernoulli Polynomials
Martin Belton
Jacobi Polynomials in an Orthogonal Collocation Method
Jorge Gamaliel Frade Chávez
Weierstrass Approximation Theorem
Fabián Alejandro Romero
Polynomial Approximation of the Exponential Function
Hein Hundal
Stirling's Approximation versus n!
Sam Nicoll
Approximation of Discontinuous Functions by Fourier Series
David von Seggern (University Nevada-Reno)
Simultaneous Approximation of Two Real Numbers by Rationals
Mateja Budin
Approximating Continuous Functions with Haar Approximations
Sijia Liang and Bruce Atwood
