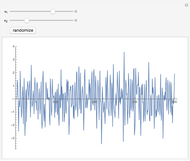
Approximation of Discontinuous Functions by Fourier Series

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
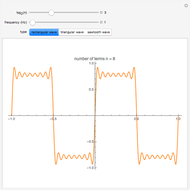
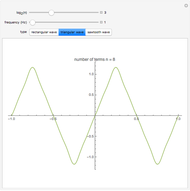
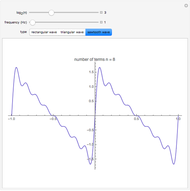
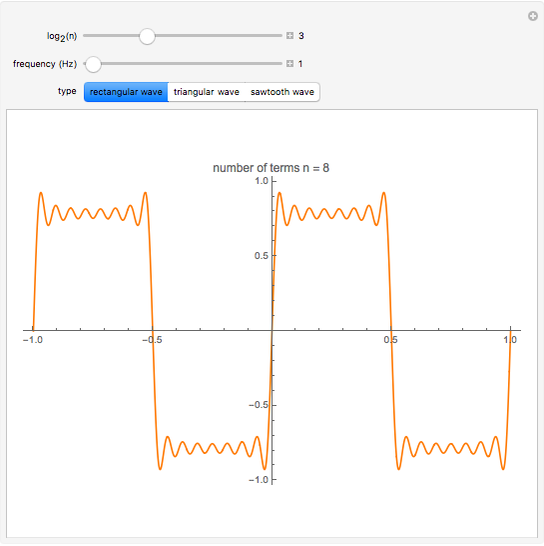
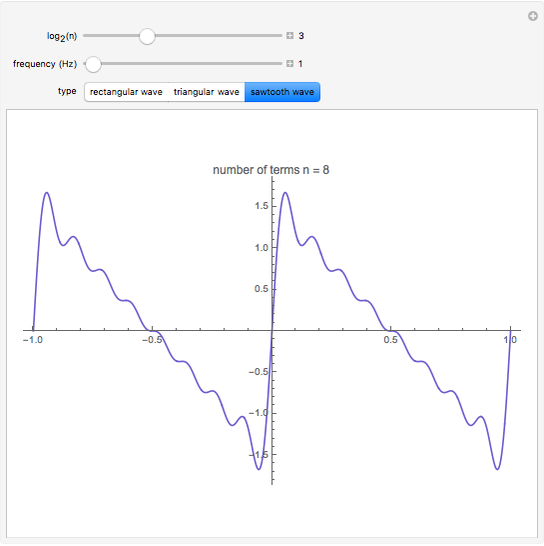
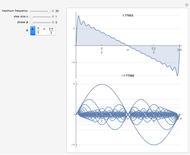
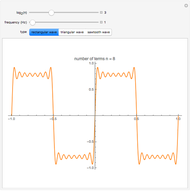
This Demonstration shows how a Fourier series of sine terms can approximate discontinuous periodic functions well, even with only a few terms in the series. Use the sliders to set the number of terms to a power of 2 and to set the frequency of the wave.
Contributed by: David von Seggern (University Nevada-Reno) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The approximations used here are sums of sine terms (Fourier sine series) given by:
(1) rectangular wave
 ,
,
(2) triangular wave
 , and
, and
(3) sawtooth wave
where  is the number of terms,
is the number of terms, 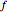 is the wave frequency (Hz), and
is the wave frequency (Hz), and  is time (seconds). These are not the only possible ways to approximate the given functions; others can be found in standard mathematical reference books.
is time (seconds). These are not the only possible ways to approximate the given functions; others can be found in standard mathematical reference books.
Truncating the series to finitely many terms introduces significant oscillations in the approximation near sharp changes in the ideal function. This effect, known as the Gibbs phenomenon, is reduced by simply using more terms. The maximum overshoot cannot be brought close to zero, but the excess area under the curve can be made arbitrarily small.
Permanent Citation