Beverton and Holt's Yield per Recruit Model

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
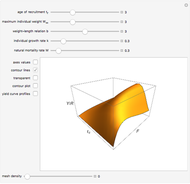
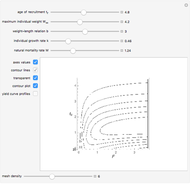
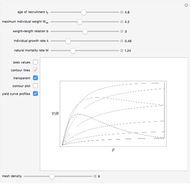
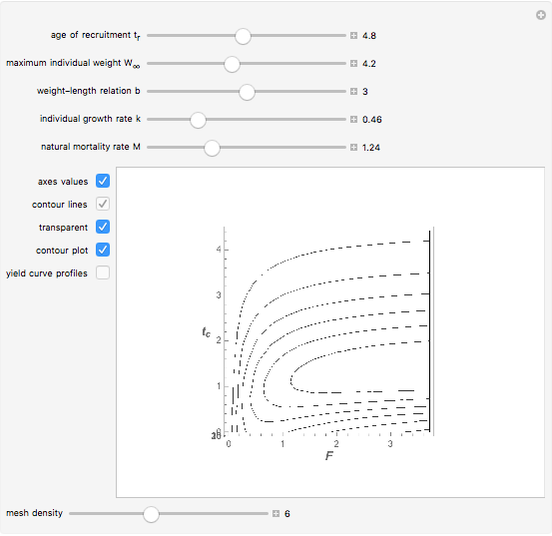
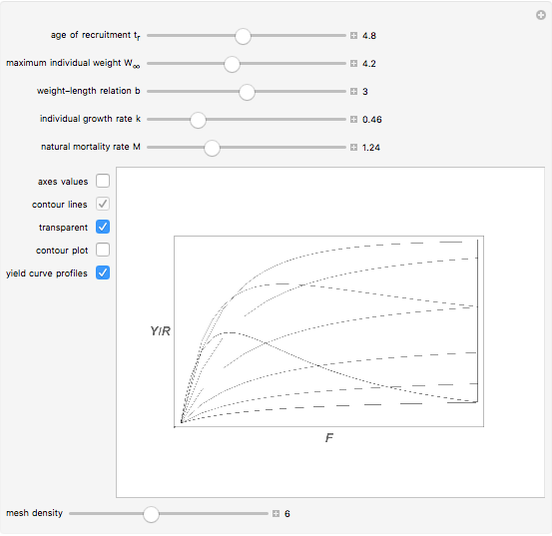
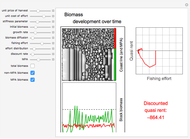
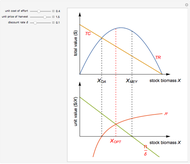
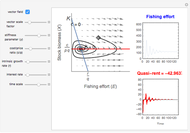
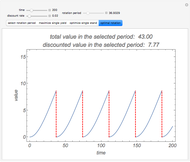
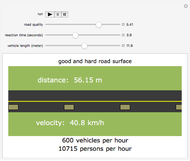
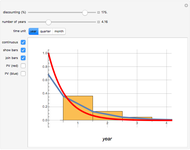
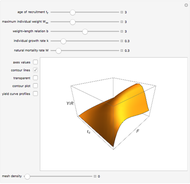
In 1957 R. J. H. Beverton and S. J. Holt published their seminal work on the dynamics of exploited fish populations. The work includes individual growth models of von Bertalanffy, mortality models of Baranov, and a number of other methods to describe population dynamics. The most famous model presented in the work of Beverton and Holt is the simple yield per recruit model, presenting the sustainable yield of a fish population as a function of age of first catch 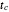 , assuming knife-sharp selection and rate of fishing mortality
, assuming knife-sharp selection and rate of fishing mortality  . The weight-length-relation
. The weight-length-relation  is assumed to be close to 3 (cubic relation) and the natural mortality rate
is assumed to be close to 3 (cubic relation) and the natural mortality rate 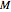 is in most cases close to the natural individual growth rate
is in most cases close to the natural individual growth rate  .
.
Contributed by: Arne Eide (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
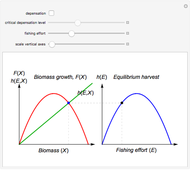
The Beverton and Holt yield per recruitment model is utilizing the individual growth model of von Bertalanffy and the Baranov mortality model. Baranov describes mortality as a continuous process in time where the number of individuals is monotonously reduced from the initial number  (number of recruits) and a fixed mortality rate (
(number of recruits) and a fixed mortality rate ( ). The number of individuals at time
). The number of individuals at time  then is
then is 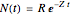 .
.
The marginal mortality rate ( ) may be decomposed into a natural component (
) may be decomposed into a natural component (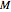 ) and mortality caused by fishing (
) and mortality caused by fishing ( ),
), 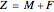 .
.  is a control variable in fisheries; when not fishing,
is a control variable in fisheries; when not fishing,  , while
, while  increases as the fishing effort is increased.
increases as the fishing effort is increased.
Another control variable in fisheries is related to how large the targeted fish is, namely the age of the fish when caught, labeled 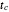 (age of first catch). Usually (as in this Demonstration) this is the age of a sudden shift in marginal mortality rate from
(age of first catch). Usually (as in this Demonstration) this is the age of a sudden shift in marginal mortality rate from  to
to 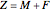 , often referred to as knife-sharp selection.
, often referred to as knife-sharp selection.
Individual fish growth is in the Demonstration modeled by the simple version of von Bertalanffy’s growth equation expressed in terms of weight, where the individual weight at time  is
is 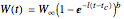 ,
,  being the length/weight relationship parameter (usually close to 3).
being the length/weight relationship parameter (usually close to 3).
Reference:
R. J. H. Beverton and S. J. Holt, On the Dynamics of Exploited Fish Populations, Caldwell, NJ: Blackburn Press, 1957 (reprint).
Permanent Citation