Surplus Production Models and Equilibrium Harvest

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
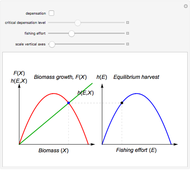
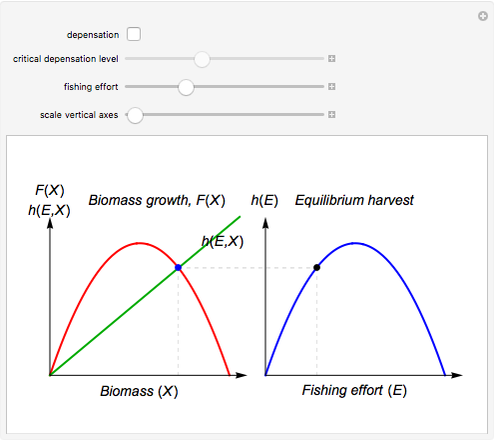
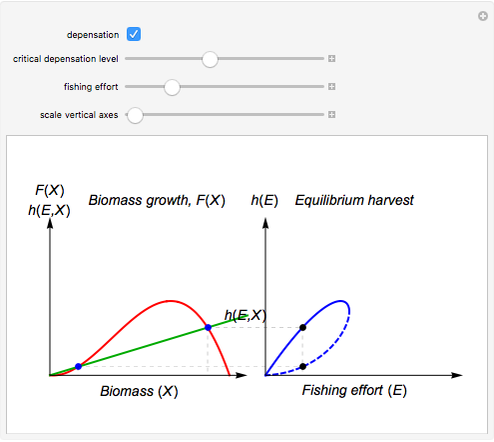
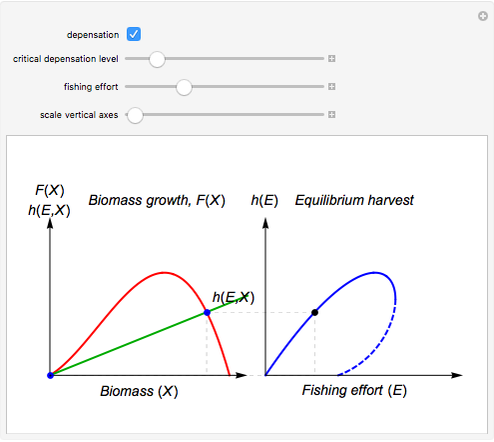
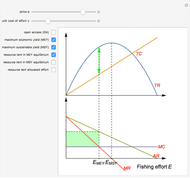
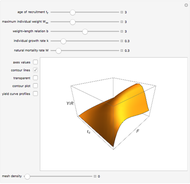
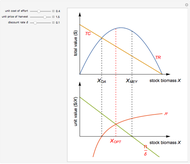
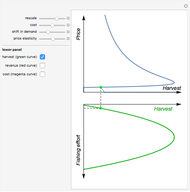
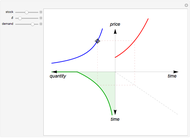
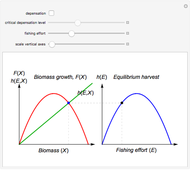
Textbook bioeconomics (here considering fisheries) assumes logistic population growth and short term harvest production to be linear in stock biomass and fishing effort. The first assumption is expressed by the growth equation 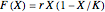 (red curve),
(red curve), 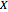 being the stock biomass and the parameters
being the stock biomass and the parameters and
and 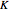 the intrinsic growth rate and the environmental saturation level, respectively.
the intrinsic growth rate and the environmental saturation level, respectively. 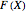 is the per period of time surplus production.
is the per period of time surplus production.  is the natural equilibrium in the absence of fishing. The second assumption is the bilinear harvest equation
is the natural equilibrium in the absence of fishing. The second assumption is the bilinear harvest equation 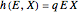 (green line),
(green line), 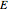 being the fishing effort, while the parameter
being the fishing effort, while the parameter  is known as the catchability coefficient. The fishing activity disturbs the natural equilibrium (
is known as the catchability coefficient. The fishing activity disturbs the natural equilibrium ( ) and each level of fishing effort includes new equilibria determined by
) and each level of fishing effort includes new equilibria determined by 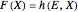 . This Demonstration illustrates how the collection of all existing equilibria found by varying values of
. This Demonstration illustrates how the collection of all existing equilibria found by varying values of 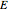 describes the equilibrium catch
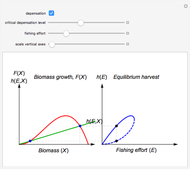
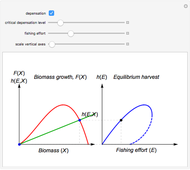
describes the equilibrium catch 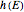 , (blue curve). Depensation (decrease in marginal growth by decreasing population biomass) may give rise to two equilibrium points, one stable and the other unstable. The dashed blue curve indicates where unstable equilibrium points are found. Positive critical depensation levels are found when depensation causes negative biomass growth. The term depensation refers to a situation where decline in biomass is not compensated by increased per unit of biomass production, as in the logistic growth equation, where
, (blue curve). Depensation (decrease in marginal growth by decreasing population biomass) may give rise to two equilibrium points, one stable and the other unstable. The dashed blue curve indicates where unstable equilibrium points are found. Positive critical depensation levels are found when depensation causes negative biomass growth. The term depensation refers to a situation where decline in biomass is not compensated by increased per unit of biomass production, as in the logistic growth equation, where 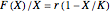 is a down-sloping line for
is a down-sloping line for 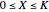 .
.
Contributed by: Arne Eide (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The term "depensation" in population growth refers to a situation where stock is unable to compensate reduced stock size by increasing growth per unit of biomass, which is normally assumed. Depensation may lead to critical low growth rates, causing stock collapses.
Permanent Citation
"Surplus Production Models and Equilibrium Harvest"
http://demonstrations.wolfram.com/SurplusProductionModelsAndEquilibriumHarvest/
Wolfram Demonstrations Project
Published: March 7 2011